Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний

Итак, на систему, находящуюся в состоянии 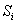, действует простейший поток событий. Как только появится первое событие этого потока, происходит «перескок» системы из состояния 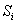в состояние 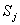(на графе состояний по стрелке ).

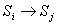Для нахождения всех вероятностей состояний 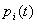как функций времени составляются и решаются уравнения Колмогорова – особого вида уравнения, в которых неизвестными функциями являются вероятности состояний. Правило составления этих уравнений приведем здесь без доказательств. Но прежде, чем его приводить, объясним понятие финальной вероятности состояния.
Финальные вероятности состояний – это уже не переменные величины (функции времени), а простые постоянные числа. Отсюда очевидно, что

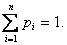
Финальная вероятность состояния 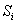– это по – существу среднее относительное время пребывания системы в этом состоянии.
Правило составления системы уравнений Колмогорова: в каждом уравнении системы в левой его части стоит финальная вероятность данного состояния 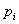, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а в правой его части – сумма произведений интенсивностей всех потоков, входящих в 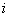- е состояние, на вероятности тех состояний, из которых они исходят.