Этап первый. СМО с отказами

 

Задачи этапа

 

На этом этапе проводитсяминимизация средней стоимостиобслуживания одной заявки в единицу времени для системы с отказами.

Требуется определить число каналов обслуживания, обеспечивающее в системе с отказами наименьшее значение параметра C – средней стоимости обслуживания одной заявки в единицу времени.

В соответствии с вариантом задания определены параметры системы λ и . Задаваясь значениями n (число каналов обслуживания) от единицы до шести, вычисляются финальные вероятности и в соответствии с ними – показатели эффективности системы. Результаты вычислений представляются в виде таблиц, формы которых приведены в приложении 2, и в виде графиков функций С = С(n), = 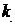(n), = (n), = (n), построенных в масштабе в зависимости от n. В качестве оптимального числа каналов следует принять такое значение n, при котором принимает наименьшее значениесредняя стоимость С обслуживания одной заявки в единицу времени (с учетом ограничения ). Следовательно, либо точка минимума на графике функции С = С(n), либо = 6, если С = С(n) – монотонно убывающая функция.

Запоминаются значения основных показателей эффективности оптимальной СМО с отказами:

= () (3.1)

= () (3.2)

= () (3.3)

Вычисляется допустимое для смешенных СМО значение времени пребывания заявки в системе

 

 

Исходные значения:

 

1) λ = 4,0 ;

 

2)

 

3) с_к = ;

 

4) с_пк = ;

 

5) с_оч = ;

 

6) с_отк = ед.стоим. * ед.врем.

 

Условия:

 

Расчетная часть

 

1)Расчет показателей эффективности для СМО с отказами при n =1;

= 0.143;

0.857;

0.143;

0.571;

0.857;

0.143;

0.857;

0.214;

1.143;

2.000;

 

Таблица 3.1- Результаты вычислений эффективности СМО с отказами

 

Система с отказами λ=4,0 1/ед врем., tобс=1,5 ед.врем., α=6,0
Результирующие показатели
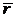
n				1/ед.вр.	1/ед.вр.	Cобщ	С			ед.вр
ед.ст	ед.ст
	0.857	0.143		3.429	0.571	1.143	2.000	0.143	0.857	0.214
	1.680	0.320		2.880	1.120	1.480	1.321	0.280	0.840	0.420
	2.459	0.541		2.361	1.639	1.810	1.104	0.410	0.820	0.615
	3.183	0.817		1.878	2.122	2.130	1.004	0.530	0.796	0.796
	3.838	1.162		1.442	2.558	2.440	0.954	0.640	0.768	0.959
	4.410	1.590		1.060	2.940	2.735	0.930	0.735	0.735	1.103

 

 

Таблицы 3.2- Результаты вычислений общей стоимости обслуживания заявок в единицу времени для СМО с отказами

 

 

К вычислению общей стоимости обслуживания заявок в единицу времени
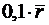n	ед. стоим.	ед.стоим.	ед.стоим.	ед.стоим.	Cобщ
ед.стоим.
	0.429	0.029		0.686	1.143
	0.840	0.064		0.576	1.480
	1.230	0.108		0.472	1.810
	1.591	0.163		0.376	2.130
	1.919	0.232		0.288	2.440
	2.205	0.318		0.212	2.735

 

 

Зависимость средней стоимости обслуживания одной заявки в единицу времени (C) от количества каналов обслуживания (n) показана на Графике 3.1

 

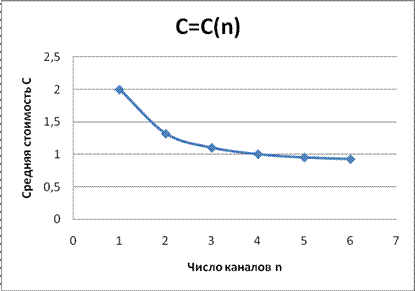
График 3.1 - График зависимости средней стоимости обслуживания одной заявки в единицу времени (C) от количества каналов обслуживания (n)

 

Зависимость вероятности обслуживания заявки (Р_обс) от количества каналов обслуживания (n) показана на Графике 3.2

 

График 3.2 - График зависимости вероятности обслуживания заявки (Р_обс) от количества каналов обслуживания (n)

 

Зависимость коэффициента загрузки системы ( от количества каналов обслуживания (n) показана на Графике 3.3

 

График 3.3 – График зависимости коэффициента загрузки системы ( от количества каналов обслуживания (n)

 

Зависимость времени пребывания заявки в системе ( от количества каналов обслуживания (n) показана на Графике 3.4

 

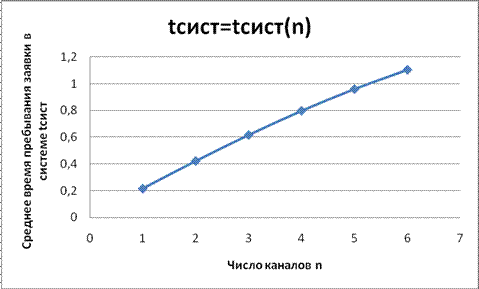
График 3.4 – График зависимости времени пребывания заявки в системе ( от количества каналов обслуживания (n)

Вывод

Вычислим допустимое для смешанных СМО значение времени пребывания заявки в системе

Вычислив показатели эффективности для СМО с отказами, учитывая число каналов обслуживания равное от единицы до шести, мы выяснили, что СМО с отказами при использовании шести каналов обслуживания является наилучшей т.к. минимальная стоимость обслуживания одной заявки в единицу времени (С) в этом случае является наименьшей. Из этого следует, что система с шестью каналами обслуживания(n=6) является оптимальной.