Задача. Если в календаре 2013 года соединить числа 10, 20 и 30 января, то получится равнобедренный прямоугольный треугольник.
Решение.
Для удобства решения задачи, используем календарь, в котором числа запишем на клетчатой бумаге.

Из построения чертежа очевидно, что треугольники с вершинами в числах 30 – 9 – 10 и 10 – 13 – 20 – прямоугольные, с прямыми углами в вершинах с числами 9 и 13 соответственно. Из чертежа ясно, что стороны 9 – 30 и 10 – 13 равны; аналогично равны стороны 9 – 10 и 13 – 20. Отсюда, треугольники 30 – 9 – 10 и 10 – 13 – 20 равны по двум катетам. Из равенства треугольников следует равенство соответствующих их сторон 10 – 30 и 10 – 20.
Так как сумма углов в треугольнике равна 180˚, получаем, что сумма острых углов в треугольнике с вершинами в числах 9 – 10 – 30 равна 90˚. Следовательно, сумма углов, дополняющих угол 10 до развернутого угла, равна сумме острых углов треугольника 9 – 10 – 30. Значит, угол 10 тоже равен 90˚. Итак, треугольник с вершинами в числах 10 – 20 – 30 является равнобедренным и прямоугольным.
Итак, данную задачу можно переформулировать в утверждение: в календаре 2013 года при соединении чисел 10, 20 и 30 января получается равнобедренный прямоугольный треугольник.
Гипотеза 1. Попробуем расширить утверждение:если в календаре любого года соединить числа 10, 20 и 30 января, то получится равнобедренный прямоугольный треугольник.
Расположение чисел 10, 20 и 30 в январе будет зависеть от того, каким днем недели будет 1 января.







Анализируя рисунки, мы видим, что существует семь различных вариантов расположения дат в январском календаре. При этом существует всего три существенно различных ситуаций расположения чисел 10, 20 и 30. Остальные получаются из первых двух, горизонтальными сдвигами треугольника.

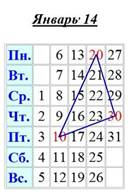

Для первого случая доказательство, что полученный треугольник – равнобедренный и прямоугольный, приведено в задаче. Рассуждения для второго случая будут аналогичными.
Вывод. Календари обладают следующей особенностью: если в календаре любого года соединить числа соответствующие 10, 20 и 30 января, то получится равнобедренный прямоугольный треугольник, за исключением случаев, где центры клеток с числами 10, 20 и 30 лежат на одной прямой.
Гипотеза 2. Попробуем расширить утверждение:если в календаре соединить числа 10, 20 и 30 любого месяца, то получится равнобедренный прямоугольный треугольник или отрезок.
Проверим это утверждение на календаре 2013 года.











Получим тоже три различных ситуации расположения чисел 10, 20 и 30 в году.
Вывод. Календари обладают следующей особенностью: если в календаре соединить числа 10, 20 и 30 любого месяца, то получится равнобедренный прямоугольный треугольник, за исключением случаев, где центры клеток с числами 10, 20 и 30 лежат на одной прямой
Заметим, что первая ситуация получается, если первое число месяца приходится на воскресенье, понедельник и вторник. Вторая ситуация получается, если первое число месяца приходится на среду, четверг и пятницу. Если первое число приходится на субботу, то получаем, что числа 10, 20 и 30 лежат на одной прямой.
Гипотеза 3. Попробуем расширить утверждение:если в календаре в любом месяце соединить числа, отстоящие друг от друга на 10 единиц, то получится равнобедренный прямоугольный треугольник или отрезок.
Проверим это утверждение на календаре 2013 года.











Из рисунков видно, что получаются треугольники или отрезки. Проведя доказательства, делаем вывод, что получаются равнобедренные прямоугольные треугольники.
Вывод. Календари обладают следующей особенностью: если в календаре любого месяца соединить числа, отстоящие друг от друга на 10 единиц, то получится равнобедренный прямоугольный треугольник, за исключением случаев, где центры клеток с числами 10, 20 и 30 лежат на одной прямой.
 2017-10-31
2017-10-31 2590
2590








