Исследование «четырехугольники в календаре»

 

Заметим, что в любом месяце можно выделить квадраты, состоящие из четырех чисел (2х2), из девяти чисел (3х3) и из шестнадцати чисел (4х4).

 

 

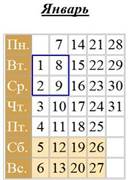
Какими свойствами обладают такие квадраты?

 

Квадрат 2х2

Свойство 1. Сумма чисел на одной диагонали выделенного квадрата, равна сумме чисел на другой диагонали.

 

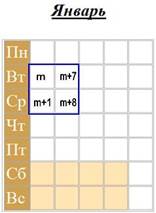
Пусть первое выделенное наименьшее число равно m, исходя из положения чисел в календаре, другие числа будут равны m + 1, m + 7 и m + 8.

Сумма одной диагонали квадрата: m + (m + 8) = 2m + 8.

Сумма другой диагонали: (m + 1) + (m + 7) = 2m + 8. Таким образом, выражения равны, а числа на одной диагонали квадрата равны сумме чисел на другой диагонали.

 

Свойство 2. Чтобы найти сумму четырех чисел в выделенном квадрате достаточно удвоить сумму чисел одной диагонали.

Свойство очевидно из предыдущего доказательства.

Пример: 2(1 + 8) = 20.

 

Квадрат 3х3

 

Свойство 1. Чтобы найти сумму девяти чисел, в выделенном квадрате календаря, необходимо к меньшему числу прибавить 8 и сумму умножить на 9.

 

 

Пусть первое выделенное наименьшее число равно m, исходя из положения чисел в календаре, другие числа будут равны m + 1, m + 2, m + 7, m + 8, m + 9, m + 14, m + 15 и m + 16.

Складывая числа, получим 9m + 72 = 9(m + 8).

Значит, сумму чисел таких квадратов можно находить, если к меньшему числу прибавить 8 и сумму умножить на 9.

 

 

Пример: (1 + 8)9 = 81.

 

Свойство 2. Чтобы найти сумму девяти чисел, в выделенном квадрате календаря, необходимо из большего числа вычесть 8 и разность умножить на 9.

 

Пусть последнее выделенное наибольшее число равно а, исходя из положения чисел в календаре, другие числа будут равны а – 1, а – 2, а – 7, а – 8, а – 9, а – 14, а – 15 и а – 16.

Складывая числа, получим: 9 а – 72 = 9(а – 8). Значит, сумму чисел таких квадратов можно находить, если из большего числа вычесть 8 и разность умножить на 9.

 

 

Пример: (17 – 8)9 = 81.

 

Квадрат 4х4

 

Свойство 1. Чтобы найти сумму шестнадцати чисел, в выделенном квадрате календаря, необходимо из большего числа вычесть 12 и полученную разность умножить на 16.

 

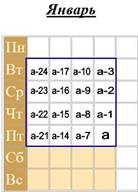
Пусть последнее выделенное наибольшее число равно а, исходя из положения чисел в календаре, другие числа будут равны а – 1, а – 2, а – 3, а – 7, а – 8, а – 9, а – 10, а – 14, а – 15, а – 16, а – 17, а – 21, а – 22, а – 23 и а – 24.

Складывая числа, получим: 16 а – 192 = 16(а – 12). Значит, сумму чисел таких квадратов можно находить, если из большего числа вычесть 12 и разность умножить на 16.

Пример: (25 – 12)16 = 208.

Свойство 2. Чтобы найти сумму 16-ти чисел достаточно умножить сумму двух чисел, стоящих на противоположенных концах любой диагонали, выделенного квадрата на 8.

 

Рассматривая квадрат из 16-ти чисел, видим, что числа в любой диагонали образуют арифметическую прогрессию с разностью 8 (а – 24, а – 16, а – 8, а) и с разностью 6 (а – 3, а – 9, а – 15, а – 21). Поэтому их сумму можно найти по формуле:
. Т.к. суммы чисел в диагоналях равны, то сумма чисел в двух диагоналях будет равна .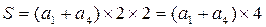

Сумма чисел в столбцах и в строках, не вошедших в диагонали, тоже равна сумме чисел в каждой диагонали. Получаем, что сумма всех чисел обведенного квадрата равна

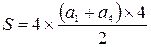или .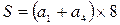

Таким образом, чтобы найти сумму 16-ти чисел достаточно умножить сумму двух чисел, стоящих на противоположенных концах любой диагонали, выделенного квадрата на 8.