Приведение вторичной обмотки к первичной

 

Так как в общем случае w₂ ¹w₁,то Е₂ ¹ Е₁ и I₂ ¹ I₁,то различны и параметры обмоток, т.е. их активные и индуктивные сопротивления, что затрудняет количественный учет процессов, происходящих в трансформаторах, и построение векторных диаграмм.

Чтобы избежать этих трудностей, обе обмотки трансформатора приводятся к одному числу витков. Обычно приводят вторичную обмотку к первичной, имеющую такое же количество витков, с условием, чтобы эта операция приведения не отразилась на энергетическом процессе. При этом число витков вторичной обмотки изменяется в «k» раз

В результате такого приведения

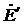₂ = k× ₂; ₂ = k× ₂. (14-21)

 

Чтобы мощность приведенной и реальной обмоток при всех режимах работы были равны, необходимо соблюдать равенство ₂× ₂ = ₂× ₂, где наведенный вторичный ток

 

₂ = ₂/k. (14-22)

 

Намагничивающие силы приведенной и реальной обмоток

 

₂×w¢₂ = ₂×w₂ (14-23)

 

Суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка, должно уменьшаться в k-раз. Но поскольку приведенная обмотка имеет в k-раз больше витков, то

 

r¢₂ = k²r₂ (14-24)

 

x¢₂ = k²x₂ (14-25)

 

Очевидно, что потери в приведенной и реальной обмотках одинаковы:

 

Одинаковы также относительные падения напряжения во вторичных обмотках приведенного и реального трансформаторов:

 

Схема замещения без учета магнитных потерь.

 

Сделаем в уравнениях (14-14) подстановки:

(14-26)

Умножив при этом второе уравнение (14-14) на k, получим

 

(14-27)

 

При переходе к электрической связи двух цепей в соответствующей схеме замещения должна появится общая для обеих цепей ветвь, которая обтекается суммой токов обеих цепей İ₁ +İ¢₂. Соответственно этому, в уравнениях напряжений этих цепей должны появиться одинаковые члены с множителями (I₁ +İ¢₂). Из уравнений (14-27) видно, что для получения в них таких членов нужно прибавить к первому уравнению и вычесть из него член jkx₁₂I¢₂. При этом:

 

(14-28)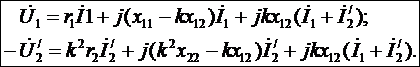

Введем следующие наименования и обозначения

- приведенное активное сопротивление вторичной обмотки

 

r¢₂=k² r ₂ (14-29)

- приведенное взаимное индуктивное сопротивление

 

x¢₁₂ = kx₁₂; (14-30)

- индуктивное сопротивление рассеяния первичной обмотки

 

x₁ = x₁₁ - k×x₁₂; (14-31)

- приведенное индуктивное сопротивление рассеяния вторичной обмотки,

 

(14-32)

 

где

(14-33)

представляет собой непреведенное индуктивное сопротивление вторичной обмотки.

В результате подстановок в (14-28) получим следующие уравнения напряжений приведенного трансформатора:

 

(14-34)

 

Этим уравнениям соответствует схема замещения рис. 14-3, а. Аналогичным образом можно также преобразовать уравнения напряжения в дифференциальной форме (14-13), произведя в них подстановки

u₂ = u¢₂/k; i₂=ki¢₂ (14-35).

 

При этом получается схема замещения рис. 14-3, б, где:

(14-36)

(14-37)

S₁ и S¢₂ представляют собой индуктивности рассеяния первичной и вторичной обмоток, а

(14-38)

приведенную взаимную индуктивность.

 

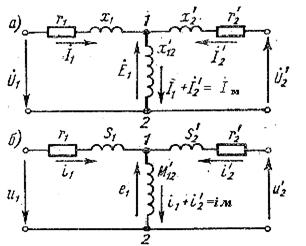
Рис. 14-3. Схемы замещения двухобмоточного трансформатора без учета магнитных потерь (Т-образные):

а) – в комплексной форме

б) – в дифференциальной форме.

 

По уравнениям (14-34) и схеме замещения рис. 14-3 получается идеальный трансформатор, у которого приведенные собственные взаимные индуктивные сопротивления одинаковы и равны

и поэтому с² = 1 и s = 0

 

Параметры схемы замещения по рис. 14-3.

При :

Приведенная взаимная индуктивность:

 

или на основании

(14-4)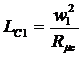

(14-39)

Последний член (14-39) весьма мал по сравнению с первым, поэтому с достаточной точностью

(14-40)

Соответственно, согласно выражениям x₁₁ = wL₁₁; x₂₂ = wL₂₂; x₁₂ = wM; x¢₁₂ = kx₁₂; и

M¢₁₂ = L_c1, , , или

(14-41)

Следовательно, сопротивление x¢₁₂ с большой точностью равно сопротивлению самоиндукции первичной обмотки от потока, замыкающегося по магнитопроводу.

Ветви 1-2 схем замещения называются намагничивающими ветвями; их ток:

, создает результирующую намагничивающую силу обмоток трансформатора: , которая в свою очередь создает результирующий поток стержня с амплитудой Ф_с.

Напряжение на этих ветвях: , т. е. равно по значению и обратно по знаку э.д.с. Е₁, которая индуктируется в первичной обмотке результирующим потоком магнитопровода и отстает от него на 90°.

Индуктивности рассеяния обмоток (без математических выкладок):

 

(14-42)

 

 

(14-43)

Таким образом, индуктивности рассеяния S₁, S₂ и S¢₂ и индуктивные сопротивления рассеяния

x₁=wS₁; x₂=wS₂; x¢₂=wS¢₂, (14-44)

при

, определяются магнитным потоком, замыкающимся главным образом по воздуху.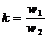

Однако вторыми членами равенств (14-42) и (14-43) по сравнению с первыми, пренебречь нельзя, и поэтому потоки, замыкающиеся по воздуху можно назвать потоками рассеяния лишь условно.

 

Схема замещения с учетом магнитных потерь.

Потери в стали магнитопровода Р_мг при заданной частоте пропорциональны величинам:

Р_мг ~ В²_с ~ Ф²_с ~ Е²₁ ~ U²₁₂,

т.е. пропорциональны квадрату напряжения U₁₂ на зажимах 1-2 намагничивающей цепи схемы замещения рис. 14-3, а. Если к этим зажимам параллельно х₁₂ = х_с1 подключить активное сопротивление r_мг, то потери в этом сопротивлении будут также пропорциональны U²₁₂. Значение сопротивления r_мг можно подобрать так, чтобы потери в нем равнялись магнитным потерям:

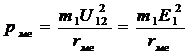
(14-45) 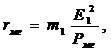Отсюда:

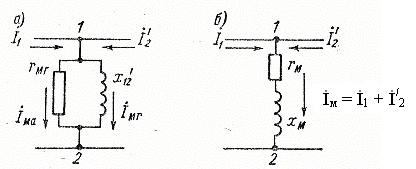
Рис. 14-4. Намагничивающая цепь с учетом магнитных потерь.

 

где m₁ – коэффициент подбора.

Намагничивающий ток _M = ₁+ ₂, разделяется в двух ветвях намагничивающей цепи на активную _МА и реактивную _МГ составляющие, из которых первая определяет мощность магнитных потерь, а вторая создает поток магнитопровода. Однако, расчеты вести удобнее, если объединить две параллельные ветви в одну общую ветвь. Тогда:

. (14-46)

 

Так как r_мг>> x¢_12, то ;

, (14-47)

При увеличении насыщения магнитопровода, т.е при увеличении Ф_с, Е₁ или U₁, приведенное индуктивное сопротивление x¢₁₂ при f = const уменьшается. Однако, при этом r_мг » const, а значение r_M уменьшается.

Схема замещения с учетом магнитных потерь согласно рис. 14-4, б показана на рис. 14-5, а. Если использовать обозначения:

 

(14-48),

 

то схему замещения можно использовать проще (рис.14-5, б).

Рис. 14-5. Схема замещения двухобмоточного трансформатора с учетом магнитных потерь.

 

В режиме холостого хода 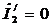и - току холостого хода.

В итоге получилась весьма простая Т-образная схема замещения трансформатора, представляющая собой пассивный четырехполюсник. Сопротивление намагничивающей цепи этой схемы z_м отражает явления в ферромагнитном магнитопроводе. Оно значительно больше сопротивления Z₁ и Z¢₂, которые включают в себя активные сопротивления и индуктивные сопротивления рассеяния обмоток. Для силовых трансформаторов в относительных единицах Z_м* = 25 ¸ 200; z_1*» z¢_2* = 0.025 ¸ 0.10.

Уравнения напряжений и схему замещения трансформатора можно представить также в относительных единицах, имея в виду что U_н = z_н × I_н.

Упрощенная схема замещения.

Поскольку z_м >> z₁» z¢₂, то можно положить во многих случаях z_м = ¥, что означает разрыв намагничивающей цепи схемы замещения, т.е. I_м = 0, что аналогично пренебрежению намагничивающим током или током холостого хода, что в ввиду малости во многих случаях допустимо. При этом

При z_м = ¥ и I_м = 0 схема замещения принимает вид, изображенный на рис. 14-6. Параметры этой схемы:

(14-49)

Рис. 14-6. Упрощенная схема замещения трансформатора

 

называются соответственно: полным, активным и индуктивным сопротивлениями короткого замыкания. Обычно в силовых трансформаторах z _k* = 0,05 ¸ 0,15.

Замыкание вторичных зажимов трансформатора накоротко, соответствует замыканию накоротко вторичных (правых) зажимов схемы замещения и при этом сопротивление трансформатора будет равным z_к.