Тема заняття: Розв’язання задач теорії ігор.
(Зведення задач теорії ігор до задач ЛП та вирішення останніх симплексним методом).
Мета: сформувати вміння та навички розв’язання задач теорії ігор симплексним методом.
Методичні рекомендації: Вивчити лекцію №6 та ознайомиться з наступною літературою [3 с. 224-250], [4 с. 239-251].
Постановка завдання:
Якщо матрична гра не має сідлової точки, то знаходження її розв’язку, особливо за великої кількості стратегій, — доволі складна задача, яку можна ефективно розв’язати методами лінійного програмування.
Задача розглядається в такому формулюванні: знайти вектори ймовірностей 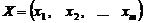 і
і  з метою визначення оптимального значення ціни гри та оптимальних стратегій.
з метою визначення оптимального значення ціни гри та оптимальних стратегій.
Зауважимо, що доведено основну теорему теорії ігор: кожна скінчена гра має принаймні один розв’язок, який можливий в області змішаних стратегій.
Отже, нехай маємо скінченну матричну гру з платіжною
матрицею
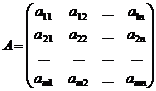 .
.
Оскільки оптимальні стратегії гравців А і В дозволяють отримати виграш
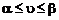 ,
,
то використання оптимальної змішаної стратегії гравцем А має забезпечувати виграш не менший за ціну гри в разі вибору гравцем В будь-яких стратегій. Математично ця умова записується так:

 . (1)
. (1)
Відповідно використання оптимальної змішаної стратегії гравцем В має за будь-яких стратегій гравця А забезпечувати програш В, що не перевищує ціни гри 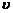 :
:

 . (2)
. (2)
Ці два співвідношення застосовують для знаходження розв’язку гри.
Отже, потрібно знайти  , щоб
, щоб

за умов
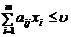
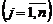 ,
,
 ,
,

 .
.
Зауважимо, що ціна гри 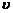 невідома і має бути визначена під час розв’язування задачі.
невідома і має бути визначена під час розв’язування задачі.
Модель ігрової задачі може бути спрощена.
З (1) маємо:

Поділивши всі обмеження на 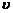 , дістанемо:
, дістанемо:
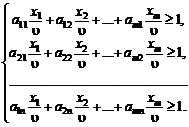
Нехай 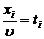 , тоді
, тоді

Згідно з умовою  , звідки
, звідки 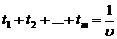 .
.
Отже, цільова функція початкової задачі набирає такого вигляду:
 .
.
У результаті задача лінійного програмування:
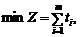 (3)
(3)
за умов
 (4)
(4)

 . (5)
. (5)
Розв’язавши цю задачу симплексним методом, знайдемо значення  , а також
, а також 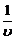 і
і  , тобто визначимо змішану оптимальну стратегію для гравця А.
, тобто визначимо змішану оптимальну стратегію для гравця А.
За аналогією запишемо задачу лінійного програмування для визначення оптимальної стратегії гравця В. Нехай
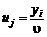
 .
.
Тоді маємо таку лінійну модель:
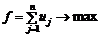
за умов
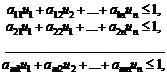
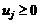
 .
.
Очевидно, що задача лінійного програмування для гравця В є двоїстою до задачі гравця А, а тому оптимальний розв’язок однієї з них визначає оптимальний розв’язок спряженої.
Розглянемо приклад на застосування методів лінійного програмування до знаходження оптимального розв’язку гри.
| Приклад 1. |
Агрофірма «Зоря» розробила шість бізнес-планів
(А 1, А 2, А 3, А 4, А 5, А 6) для реалізації в наступному році. Залежно від зовнішніх умов (погодних умов, стану ринку тощо) виокремлено п’ять ситуацій (В 1, В 2, В 3, В 4, В 5). Для кожного варіанту Аі  бізнес-плану та зовнішньої ситуації
бізнес-плану та зовнішньої ситуації 
 обчислено прибутки, наведені в такій таблиці:
обчислено прибутки, наведені в такій таблиці:
| Варіант бізнес-плану | Зовнішні ситуації | ||||
| В 1 | В 2 | В 3 | В 4 | В 5 | |
| Прибутки тис. грн. | |||||
| А 1 | 1,0 | 1,5 | 2,0 | 2,7 | 3,2 |
| А 2 | 1,2 | 1,4 | 2,5 | 2,9 | 3,1 |
| А 3 | 1,3 | 1,6 | 2,4 | 2,8 | 2,1 |
| А 4 | 2,1 | 2,4 | 3,0 | 2,7 | 1,8 |
| А 5 | 2,4 | 2,9 | 3,4 | 1,9 | 1,5 |
| А 6 | 2,6 | 2,7 | 3,1 | 2,3 | 2,0 |
Потрібно вибрати варіант бізнес-плану або комбінацію з розроблених планів.
Розв’язування. Маємо гру, платіжною матрицею якої є відповідні елементи наведеної таблиці. Легко переконатися, що домінуючих стратегій у цій грі немає.
Далі визначаємо:
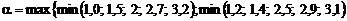 ;
;
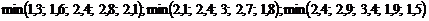 ;
;
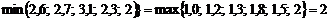 ,
,
а також
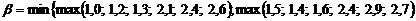 ;
;
 ;
;
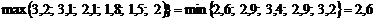 .
.
Отже, 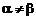 , тобто сідлової точки немає, а це означає, що потрібно скористатися моделлю (3)—(5):
, тобто сідлової точки немає, а це означає, що потрібно скористатися моделлю (3)—(5):

за умов
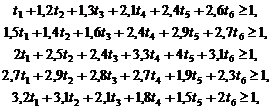

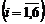 .
.
Розв’язуємо цю задачу симплексним методом.
Задача 1
Підприємство виготовляє три види продукції А1, А2, А3, отримуючи при цьому прибуток, що залежить від попиту. Попит може перебувати в одному з чотирьох станів В1, В2, В3, В4. Прибуток підприємства, який отриманий при виготовленні кожного виду продукції в залежності від попиту, наведено у наступній таблиці:
| Вj Аi | В1 | В2 | В3 | В4 |
| А1 | ||||
| А2 | ||||
| А3 |
Визначити оптимальні обсяги виготовлення продукції, які гарантуватимуть середню величину прибутку при будь-якому попиті, вважаючи його невизначеним.
Задача 2
Швейне підприємство планує масове виготовлення нової моделі одягу. Попит на цю модель не може буди точно визначений, тобто, його величина характеризується трьома можливими станами: І, ІІ, ІІІ. У залежності від цих станів аналізуються три можливих варіанти виготовлення цієї моделі: А, В, С. Кожний з цих варіантів вимагає своїх витрат і має різну ефективність. Прибуток (тис.грн.), який отримає підприємство при заданому обсязі виготовлення моделі одягу і відповідному стані попиту, визначається матрицею:
| І | ІІ | ІІІ | |
| А | |||
| В | |||
| С |
Необхідно визначити обсяг виготовлення моделі одягу, що забезпечує середню величину прибутку при будь-якому стані попиту.
Задача 3
Побудувати гру, задану задачею лінійного програмування:
3.1.  ; 3.2.
; 3.2. 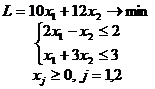 .
.
ДОДАТКОВІ ЗАВДАННЯ:
Задача 4
Взуттєва фабрика планує виготовлення двох моделей взуття А і В. попит на ці моделі невизначений, і може перебувати в одному із станів: І, ІІ. В залежності від цих станів прибуток фабрики різний і визначається матрицею:
| І | ІІ | |
| А | ||
| В |
Знайти оптимальне співвідношення між обсягами виготовлення кожної із моделей взуття, за яким фабриці гарантується середня величина прибутку при будь-якому попиті.
Задача 5
Торгівельне підприємство розробило декілька варіантів плану продажі товарів на ярмарці з врахуванням кон’юнктури ринку і попиту покупців, які постійно змінюються. Доходи підприємства в залежності від цих показників наведені у таблиці:
| План продажі товарів | Величина доходу, ум.од. | ||
| S1 | S2 | S3 | |
| P1 | |||
| P2 | |||
| P3 |
Визначити оптимальний план продажі товарів на ярмарці.
Задача 6
Побудувати гру, задану задачею лінійного програмування:
6.1.  .
.
 2018-01-21
2018-01-21 505
505








