Тема 6. Нелінійні оптимізаційні моделі економічних систем

ЛАБОРАТОРНЕ ЗАНЯТТЯ №22.

Тема заняття: Розв’язання задач нелінійного програмування класичним методом.

Мета: сформувати вміння та навички розв’язання задач нелінійного програмування класичним методом.

Методичні рекомендації: Вивчити лекцію №7 та ознайомиться з наступною літературою [2 с. 183-208], [3 с. 252-294].

Постановка завдання:

Знайти такий вектор 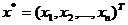, що належить області допустимих рішень 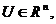цільова функція від якого

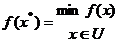
Зауваження:

1. Пошук максимуму функції зводиться до задачі визначення мінімуму функції шляхом заміни знака перед функцією на протилежний: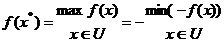

2. Задача пошуку максимуму та мінімуму цільової функції зветься задачею пошуку екстремуму: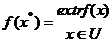

3. Якщо безліч допустимих рішень U задається обмеженнями, що накладаються на вектор х, то вирішується завдання пошуку умовного екстремуму. Якщо, обмеження на вектор х відсутні, то вирішується завдання пошуку безумовного екстремуму.

4. Рішенням задачі пошуку екстремуму є пара 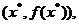яка включає точку х^* та значення цільової функції f в цій точці.

Нагадаємо, що точка 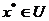зветься точкою глобального мінімуму (або просто мінімуму), якщо на множені U функція досягає свого мінімального значення, тобто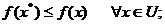

точка 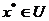зветься точкою локального мінімуму функції f на множені U, якщо 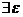>0, щ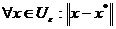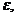о < то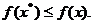

Тут 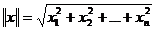- евклідова норма вектора х.