1. Для того щоб матриця Гессе Н (х*) була позитивно визначеною і стаціонарна точка х* була точкою локального мінімуму, необхідно і достатньо, щоб знаки кутових мінорів були строго додатні:
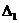 >0,
>0, 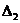 >0, ….,
>0, …., 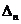 >0.
>0.
2. Для того щоб матриця Гессе Н (х*) була негативно певної і стаціонарна точка х* була точкою максимуму, необхідно і достатньо, щоб знаки кутових мінорів чергувалися, починаючи з негативного
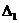 <0,
<0, 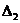 >0,…,(-1)n
>0,…,(-1)n 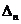 >0.
>0.
Приклад 1. Дослідити функцію f ( ) = x 13 – 2 x 1 x 2 + x 23 на опуклість (вгнутість). Знайдемо частинні похідні:
) = x 13 – 2 x 1 x 2 + x 23 на опуклість (вгнутість). Знайдемо частинні похідні:
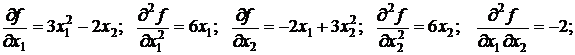
Запишемо матрицю Н та обчислимо головні мінори.
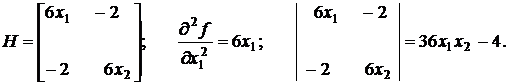
Якщо x 1 > 0 i x 2 >  , то функція f (
, то функція f ( ) = x 13 – 2 x 1 x 2 + x 23 опукла. Якщо x 1 < 0 i x 2 >
) = x 13 – 2 x 1 x 2 + x 23 опукла. Якщо x 1 < 0 i x 2 >  , то функція строго вгнута, бо визначник першого порядку
, то функція строго вгнута, бо визначник першого порядку 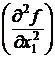 від’ємний, а визначник другого порядку – додатний.
від’ємний, а визначник другого порядку – додатний.
Приклад 2.
Знайти екстремум функції 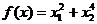 на множені R2:
на множені R2:
1. Записуємо необхідні умови екстремуму першого порядку

З системи рівнянь знаходимо стаціонарну точку  .
.
Перевіряємо виконання достатніх умов екстремуму другого порядку.
Матриця Гессе в точці х* має вигляд  .
.
Оскільки 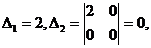 то достатні умови екстремуму не виконуються. Необхідні додаткові дослідження.
то достатні умови екстремуму не виконуються. Необхідні додаткові дослідження.
Задача 1
Знайти екстремуми функції:
1.1. Z = 2х2 + ху + у2 + х – у + 1;
1.2. Z = х12 + х22, при умові х1 + х2 = 5;
1.3. Ціни за одиницю кожної з послуг становлять відповідно 10 і 20 гр. од. Капітал споживача – 1700 гр. од. Необхідно оптимально розділити капітал між цими послугами, якщо індивідуальна функція споживача має вигляд:
f (х1, х2) = 2 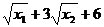 ;
;
1.4. Z = х12 - х22 при умові 3х1 + 4х2 = 12;
1.5. Z = 2х12 + 3х22 + х32, при умові х1 + х2 + х3 = 8;
1.6. Z = х1 х2, при умові х1 + х2 = 1.
 2018-01-21
2018-01-21 711
711








