Свойства плотности распределения

1. Плотность распределения есть неотрицательная функция:

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

Геометрически эти свойства означают, что:

1) Вся кривая распределения лежит не ниже оси абсцисс

2) Полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Пример:

Функция распределения непрерывной случайной величины X задана выражением

Найти:

а) Коэффициент a

б) Плотность распределения f(x)

в) Вероятность попадания величины X на участок от 0,25 до 0,5

Решение:

а) Так как функция распределения величины X непрерывна, то при откуда

б) Плотность распределения величины X выражается формулой

в) Вероятность попадания

Пример:

Случайная величина X подчинена закону распределения с плотностью при

Найти:

а) Коэффициент а

б) Построить график плотности распределения

в) Найти функцию распределения F(x) и построить ее график

г) Определить вероятность попадания на участок от 0 до

Решение:

а) Для определения коэффициента а воспользуемся свойством плотности распределения

откуда

б) График плотности распределения:

Рисунок 12

в) По формуле 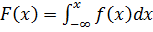получаем выражение функции распределения

Рисунок 13

г) Вероятность попадания величины X на заданный отрезок