2018-01-21
692
Т.к. напряженное состояние однородно, то однородным будет и деформированное состояние. Любой элемент объема будет деформироваться одинаково. Поперечные сечения стержня останутся плоскими, и будут удаляться друг от друга при растяжении и сближаться при сжатии. Этот факт можно положить в основу всей теории и сформулировать как гипотезу плоских сечений: сечения плоские и нормальные к оси до деформации остаются плоскими и нормальными к оси после деформации.
Определим удлинения и деформации, возникающие в стержне.
Пусть 
- длина стержня до деформации, 
- длина стержня после деформации. Величину 
называют продольным удлинением. Т.к. деформированное состояние однородно, то деформация не зависит от базы измерения. Деформация в направлении оси стержня равняется: 
(2) Эта величина называется относительным удлинением стержня.
Продольная деформация (в направлении оси стержня) сопровождается поперечной: 
, где 
- характерный размер поперечного сечения до деформации;
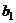- то же самое после деформации.
Знаки продольной и поперечной деформаций противоположны. Продольное удлинение сопровождается уменьшение поперечных
размеров и наоборот.
Отношение деформации поперечной к деформации продольной есть для данного материала величина постоянная, называется коэффициентом Пуассона. 
Оценим величину коэффициента Пуассона. При растяжении стержня его длина увеличилась в отношении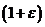 
, а линейные размеры сечения уменьшились в отношении 
, следовательно, площадь поперечного сечения уменьшилась в отношении 
. Относительное изменение объема равно: 
Т.к. деформации малы, то удержим в выражении лишь их первые степени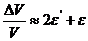 
. Т.к. при растяжении объем должен увеличиться, то 
т.е.
коэффициент Пуассона по величине не превышает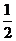 
.
Для сталей эта величина колеблется в пределах 0,25 – 0,35.
