Связь между напряжениями и деформациями

Закон Гука.

Как уже упоминалось ранее, между напряжениями и деформа

циями существует связь, которая может быть установлена лишь экспериментальным путем.

Большинство твердых тел, при сравнительно небольших нагрузках, обнаруживают свойство однозначной зависимости между напряжениями и деформациями (или между силами и перемещениями).

Например, если вспомнить известные нам из курса лабораторных работ диаграммы растяжения и сжатия малоуглеродистой стали, то можно заметить, что вплоть до значений напряжения равного - предела пропорциональности зависимость между напряжениями и деформациями близка к линейной.

Подобная картина наблюдается и у других сталей, а также, может быть менее отчетливо, у других материалов. Данный экспериментальный факт позволяет принять простейший из упругих законов – закон Гука, т.е. закон линейной упругости:

Напряжения пропорциональны деформациям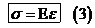

Коэффициент пропорциональности между напряжениями и деформациями называется модулем упругости первого рода (модулем Юнга). Модуль упругости определяется опытным путем и служит мерой жесткости материала. Геометрический смысл - угловой коэффициент прямолинейного начального участка диаграммы материала.

Модуль упругости для некоторых, часто применяемых материалов, имеет приблизительно следующие значения.

Сталь: ; Медь: ;

Дерево: ; Каучук: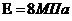

Отметим еще раз, что свойство упругости, в частности линей-

ной упругости, относительно. Уместно говорить не о упругих и неупругих материалах, а о упругом и неупругом состоянии материала.

Если в (3) выразить по формуле (2) и учесть (1), то получим закон Гука в форме, позволяющей находить удлинения.

Величину называют жесткостью при растяжении-сжатии. Закон (4) можно сформулировать следующим образом: удлинение стержня прямо пропорционально нормальной силе и длине стержня и обратно пропорционально жесткости при растяжении-сжатии.

По формуле (4) можно определять удлинения только в том

случае, если нормальная сила и поперечное сечение постоянны по

длине стержня, т.е. если напряженное состояние однородно.

Если нормальная сила и поперечное сечение меняются по длине ступенчато, то стержень надо разбить на участки, так чтобы в пределах каждого участка и были постоянны, определить удлинение каждого из участков и тогда полное удлинение стержня будет равняться алгебраической сумме, (знак определяется знаком ) удлинений участков.

Если же напряженное состояние в стержне неоднородно, то выделив малый элемент длиной определим его удлинение

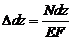, Здесь и 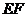рассматривается как функции z. Полное удлинение стержня будет равно:

. Напряженное состояние при растяжении и сжатии.

Во вводной лекции мы уже упоминали о напряженном состоянии в точке и в частности, говорили, что знать напряженное состояние в точке – это уметь вычислить напряжения по любой площадке, проходящей через данную точку. Теперь уже мы рассмотрим этот вопрос в случае, когда исследуемая точка принадлежит растянутому или сжатому стержню.

Пусть стержень растянут силой F и в поперечных сечениях стержня, как мы знаем, возникают нормальные напряжения равные , где А - площадь поперечного сечения.

Проведем через исследуемую точку А произвольное сечение, положение которого задается углом между осью стержня и внешней нормалью к сечению. Кроме того, проведем еще поперечное сечение. Выделим с помощью указанных сечений элемент и рассмотрим равновесие данного элемента.

По наклонной площадке действует полное напряжение . проектируя силы, действующие на элемент на ось стержня, получаем

Разлагая на нормальное и касательное напряжение, получаем

Переходя к функциям угла имеем

Уравнения (5) дают возможность вычислить напряжения по любым площадкам, проходящим через данную точку, т.е. определяют напряженное состояние при растяжении и сжатии. Очевидно, что касательные напряжения обращаются в нуль по двум площадкам (поперечное сечение) и (продольное сечение). Площадки, по которым касательные напряжения равны нулю, называются главными площадками, а нормальные напряжения, действующие по ним, главными напряжениями.

Очевидно, что одно из главных напряжений, действующее в поперечном сечении - является максимальным по модулю, что обосновывает использование формулы (1), как основной расчетной формулы при растяжении, сжатии, а другое главное напряжение, действующее в продольных площадках рано нулю. Таким образом, продольные площадки свободны от напряжений.