Теорема 4.2.4. Загальний розв’язок лінійної однорідної системи представляється у вигляді лінійної комбінації п -лінійно незалежних розв’язків.
Доведення. Як випливає з властивості 3, лінійна комбінація розв’язків також буде розв’язком. Покажемо, що цей розв’язок загальний, тобто завдяки вибору коефіцієнтів 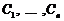 можна розв’язати будь-яку задачу Коші
можна розв’язати будь-яку задачу Коші 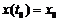 або в координатній формі:
або в координатній формі: 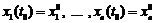 .
.
Оскільки розв’язки 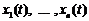 лінійно незалежні, то визначник Вронського відмінний від нуля. Отже, система алгебраїчних рівнянь
лінійно незалежні, то визначник Вронського відмінний від нуля. Отже, система алгебраїчних рівнянь
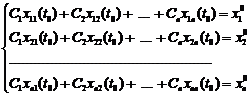 має єдиний розв’язок
має єдиний розв’язок 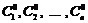 . Тоді лінійна комбінація
. Тоді лінійна комбінація
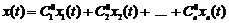
є розв’язком поставленої задачі Коші. Теорема доведена.
Властивість 1. Максимальне число незалежних розв’язків дорівнює кількості рівнянь.
Це випливає з теореми про загальний розв’язок системи однорідних рівнянь, тому що будь-який інший розв’язок може бути представлений у вигляді лінійної комбінації 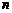 лінійно незалежних розв’язків.
лінійно незалежних розв’язків.
Визначення. Матриця, складена з будь-яких 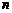 -лінійно незалежних розв’язків, називається фундаментальною матрицею розв’язків системи.
-лінійно незалежних розв’язків, називається фундаментальною матрицею розв’язків системи.
Якщо лінійно незалежними розв’язками будуть
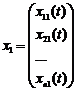 ,
, 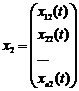 , …,
, …, 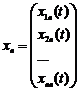 , то матриця
, то матриця 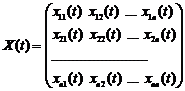
буде фундаментальною матрицею розв’язків. Як випливає з попередньої теореми загальний розв’язок може бути представлений у вигляді 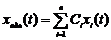 , де
, де 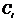 - довільні сталі. Якщо ввести вектор
- довільні сталі. Якщо ввести вектор 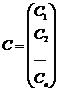 , то загальний розв’язок можна записати у вигляді
, то загальний розв’язок можна записати у вигляді 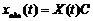 .
.
 2018-01-21
2018-01-21 463
463








