Властивості розв’язків лінійних однорідних систем

Властивість 4.2.1. Якщо вектор 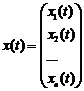є розв’язком лінійної однорідної системи, то і 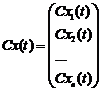, де - стала скалярна величина, також є розв’язком цієї системи. Дійсно, за умовою

. Але тоді і

оскільки дорівнює нулю вираз в дужках. Тобто є розв’язком однорідної системи.

Властивість 4.2.2. Якщо дві векторні функції 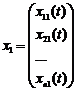, 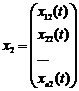є розв’язками однорідної системи, то і їхня сума також буде розв’язком однорідної системи. Дійсно, за умовою і Але тоді і

тому що дорівнюють нулю вираз в дужках, тобто є розв’язком однорідної системи.

Властивість 4.2.3. Якщо вектори , …, є розв’язками однорідної системи, та і їхня лінійна комбінація з довільними коефіцієнтами також буде розв’язком однорідної системи. Дійсно, за умовою . Але тоді і

тому що дорівнює нулю кожний з доданків, тобто є розв’язком однорідної системи.

Властивість 4.2.4. Якщо комплексний вектор з дійсними елементами є розв’язком однорідної системи, то окремо дійсна та уявна частини є розв’язками системи. Дійсно за умовою

Розкривши дужки і зробивши перетворення, одержимо

А комплексний вираз дорівнює нулю тоді і тільки тоді, коли дорівнюють нулю дійсна і уявна частини, тобто

що і було потрібно довести.

Визначення 4.2.1. Вектори , , …, називаються лінійно залежними на відрізку , якщо існують не всі рівні нулю сталі , такі, що при .

Якщо тотожність справедлива лише при 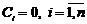, то вектори лінійно незалежні.

Визначення 4.2.2. Визначник, що складається з векторів , тобто

називається визначником Вронського.