Метод варіації довільної сталої полягає в тому, що розв’язок неоднорідного рівняння шукається в такому ж вигляді, як і розв’язок однорідного, але сталі 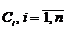 вважаються невідомими функціями. Нехай загальний розв’язок лінійного однорідного рівняння
вважаються невідомими функціями. Нехай загальний розв’язок лінійного однорідного рівняння  записано у вигляді
записано у вигляді  .
.
Розв’язок лінійного неоднорідного рівняння  шукаємо у вигляді
шукаємо у вигляді 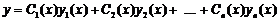 , де
, де  - невідомі функції. Оскільки підбором
- невідомі функції. Оскільки підбором 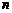 - функцій необхідно задовольнити одному рівнянню, тобто одній умові, то
- функцій необхідно задовольнити одному рівнянню, тобто одній умові, то  умову можна накласти довільно. Розглянемо першу похідну від записаного розв’язку
умову можна накласти довільно. Розглянемо першу похідну від записаного розв’язку  і зажадаємо, щоб
і зажадаємо, щоб  . Розглянемо другу похідну
. Розглянемо другу похідну 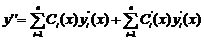 і зажадаємо, щоб
і зажадаємо, щоб  . Продовжимо процес взяття похідних до
. Продовжимо процес взяття похідних до  -ї
-ї 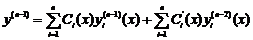 і зажадаємо, щоб
і зажадаємо, щоб  . На цьому
. На цьому  - умова вичерпалася. І для
- умова вичерпалася. І для 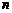 -ї похідної справедливо
-ї похідної справедливо  .
.
Підставимо взяту функцію та її похідні в неоднорідне диференціальне рівняння
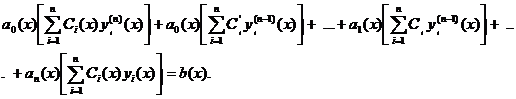 Оскільки
Оскільки  - розв’язок однорідного диференціального рівняння, то після скорочення одержимо
- розв’язок однорідного диференціального рівняння, то після скорочення одержимо
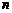 -у умову
-у умову  Додаючи перші
Додаючи перші  - умови, одержимо систему
- умови, одержимо систему

Оскільки визначником системи є визначник Вронського і він відмінний від нуля, то система має єдиний розв’язок

І загальний розв’язок лінійного неоднорідного диференціального рівняння запишеться у вигляді
 , де
, де 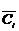 - довільні сталі,
- довільні сталі,
а 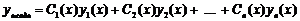 . Якщо розглядати диференціальне рівняння другого порядку
. Якщо розглядати диференціальне рівняння другого порядку
 і загальний розв’язок однорідного рівняння має вигляд
і загальний розв’язок однорідного рівняння має вигляд 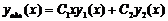 , то частинний розв’язок неоднорідного має вигляд
, то частинний розв’язок неоднорідного має вигляд  . І для знаходження функцій
. І для знаходження функцій 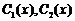 маємо систему
маємо систему 
Звідси 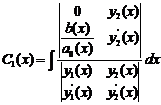 ,
, 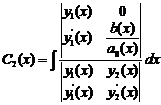 . І одержуємо
. І одержуємо 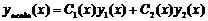 з обчисленими функціями
з обчисленими функціями  і
і  .
.
4. Системи лінійних диференціальних рівнянь з сталими коефіціентами. Знаходження загального розв’язку однорідних систем.
Загальна теорія
Система диференціальних рівнянь, що записана у вигляді
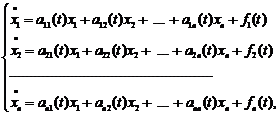
називається лінійною неоднорідною системою диференціальних рівнянь.
Система 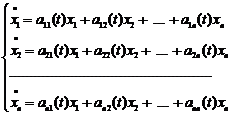 називається лінійною однорідною системою диференціальних рівнянь. Якщо ввести векторні позначення
називається лінійною однорідною системою диференціальних рівнянь. Якщо ввести векторні позначення  ,
, 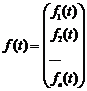 ,
, 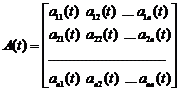 ,
,
то лінійну неоднорідну систему можна переписати у вигляді  а лінійну однорідну систему у вигляді
а лінійну однорідну систему у вигляді  . Якщо функції
. Якщо функції  неперервні в околі точки
неперервні в околі точки  , товиконані умови теореми існування та єдиності розв’язку задачі Коші, і існує єдиний розв’язок
, товиконані умови теореми існування та єдиності розв’язку задачі Коші, і існує єдиний розв’язок
 системи рівнянь, що задовольняє початковим даним
системи рівнянь, що задовольняє початковим даним

 2018-01-21
2018-01-21 500
500








