Властивості розв’язків лінійних неоднорідних рівнянь. Загальний розв’язок лінійного неоднорідного рівняння

Властивість 1. Якщо - розв’язок лінійного однорідного рівняння, - розв’язок неоднорідного рівняння, то 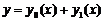буде розв’язком лінійного неоднорідного диференціального рівняння.

Дійсно, нехай і - розв’язки відповідно однорідного і неоднорідного рівнянь, тобто

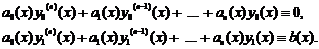
Тоді

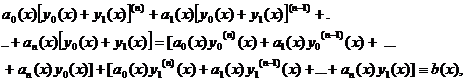
тобто 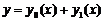- розв’язок неоднорідного диференціального рівняння.

Властивість 2 (принцип суперпозиції). Якщо - розв’язки лінійних неоднорідних диференціальних рівнянь , , то 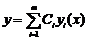з довільними сталими 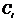буде розв’язком лінійного неоднорідного рівняння 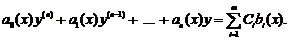Дійсно, нехай 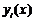- розв’язки відповідних неоднорідних рівнянь, тобто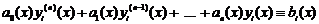

Склавши лінійну комбінацію з рівнянь і їхніх правих частин з коефіцієнтами 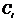одержимо

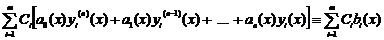або, перегрупувавши, запишемо

що і було потрібно довести.

Властивість 3. Якщо комплексна функція 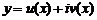з дійсними елементами є розв’язком лінійного неоднорідного рівняння з комплексною правою частиною 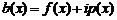, то дійсна частина 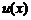є розв’язком рівняння з правою частиною , а уявна 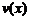є розв’язком рівняння з правою частиною .

Дійсно, як випливає з умови,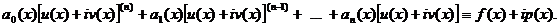

Розкривши дужки, одержимо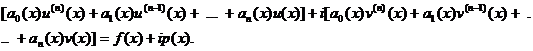

А комплексні вирази дорівнюють між собою тоді і тільки тоді, коли дорівнюють окремо дійсні та уявні частини, тобто

що і було потрібно довести.

1. Теорема про загальний розв’язок лінійного неоднорідного диференціального рівняння.

Теорема. Загальний розв’язок лінійного неоднорідного диференціального рівняння складається з загального розв’язку лінійного однорідного рівняння і частинного розв’язку неоднорідного рівняння.

Теорема (існування та єдиності розв’язку задачі Коші рівняння, не розв’язаного відносно похідної). Нехай у деяком замкненому околі точки 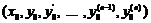функція 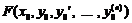задовольняє умовам:

1) вона визначена і неперервна по всім змінним;

2) 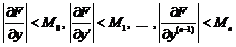; 3) .

Тоді при 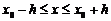, де 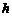- досить мала величина, існує і єдиний розв’язок 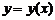рівняння , що задовольняє початковим умовам

.

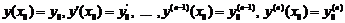Визначення. Загальним розв’язком диференціального рівняння 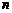-го порядку називається 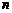-раз неперервно диференційована функція , що обертає при підстановці рівняння в тотожність, у якій вибором сталих 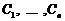можна одержати розв’язок довільної задачі Коші в області існування та єдиності розв’язків.