Властивості розв’язків лінійних неоднорідних систем

Властивість 1. Якщо вектор є розв’язком лінійної неоднорідної системи, a розв’язком відповідної лінійної однорідної системи, то сума - є розв’язком лінійної неоднорідної системи. Дійсно, за умовою і . Але тоді і

тобто є розв’язком неоднорідної системи.

Властивість 2 (Принцип суперпозиції). Якщо вектори 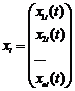, є розв’язками лінійних неоднорідних систем , , де , то вектор 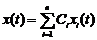, де 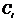-довільні сталі буде розв’язком лінійної неоднорідної системи . Дійсно, за умовою виконуються 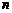- тотожностей

. Склавши лінійну комбінацію з лівих і правих частин, одержимо

, тобто лінійна комбінація 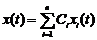буде розв’язком системи

Властивість 3. Якщо комплексний вектор з дійсними елементами є розв’язком неоднорідної системи , де , , 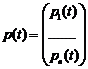, то окремо дійсна і уявна частини є розв’язками системи. Дійсно, за умовою .

Розкривши дужки і перетворивши, одержимо .

Але комплексні вирази рівні між собою тоді і тільки тоді, коли рівні дійсні та уявні частини, що і було потрібно довести.