Теорема про загальний розв’язок систем лінійних неоднорідних диференціальних рівнянь

Теорема (про загальний розв’язок лінійної неоднорідної системи). Загальний розв’язок лінійної неоднорідної системи складається із суми загального розв’язку однорідної системи і якого-небудь частинного розв’язку неоднорідної системи.

Доведення. Нехай - загальний розв’язок однорідної системи і - частинний розв’язок неоднорідної. Тоді, як випливає з властивості 1, їхня сума буде розв’язком неоднорідної системи.

Покажемо, що цей розв’язок загальний, тобто підбором сталих 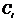, можна розв’язати довільну задачу Коші . Оскільки - загальний розв’язок однорідного рівняння, то вектори 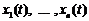лінійно незалежні і система алгебраїчних рівнянь

має єдине розв’язок , . І лінійна комбінація с отриманими сталими , є розв’язком поставленої задачі Коші.

Метод варіації довільної сталої знаходження частинного розв’язку лінійних неоднорідних систем. Формула Коші.