Побудова частинного розв’язку неоднорідної системи методом варіації довільних сталих

Як випливає з останньої теореми, для побудови загального розв’язку неоднорідної системи потрібно розв’язати однорідну і яким-небудь засобом знайти частинний розв’язок неоднорідної системи. Розглянемо метод, який називається методом варіації довільної сталої. Нехай маємо систему і - загальний розв’язок однорідної системи. Розв’язок неоднорідної будемо шукати в такому ж вигляді, але вважати 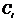не сталими, а невідомими функціями, тобто і ,чи в матричній формі , де - фундаментальна матриця розв’язків, -вектор з невідомих функцій. Підставивши в систему, одержимо , чи

. Оскільки - фундаментальна матриця, тобто матриця складена з розв’язків, то . і залишається система рівнянь . Розписавши покоординатно, одержимо Оскільки визначником системи є визначник Вронського і він не дорівнює нулю, то система має єдиний розв’язок і функції визначаються в такий спосіб

…

Звідси частинний розв’язок неоднорідної системи має вигляд . Для лінійної неоднорідної системи на площині метод варіації довільної сталої реалізується таким чином.

Нехай . Фундаментальна матриця розв’язків однорідної системи. Тоді частинний розв’язок неоднорідної шукається у вигляді Звідси І загальний розв’язок має вигляд , , де - довільні сталі.

Формула Коші

Нехай - фундаментальна система, нормована при тобто , де - одинична матриця. Загальний розв’язок однорідної системи має вигляд . Вважаючи невідомою вектором-функцією і повторюючи викладення методу варіації довільної постійний, одержимо

Звідси . Проінтегруємо отриманий вираз .

Тут - вектор із сталих, що отриманий при інтегруванні системи. Підставивши у вихідний вираз, одержимо:

Якщо - фундаментальна матриця, нормована при , то . Звідси

Підставивши початкові значення 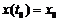і з огляду на те, що , одержимо - формулу Коші, загального розв’язку неоднорідного рівняння. Частинний розв’язок неоднорідного рівняння, що задовольняє нульовій початковій умові, має вид . Якщо система з сталою матрицею , то . І формула Коші має вигляд .