Определение кратчайших путей и маршрутов в графе с использованием алгоритма Дейкстры

В ориентированном графе путь из начальной вершины s в конечную t называется минимальным или кратчайшим, если он имеет минимальную длину среди всех путей из вершины s в t.

Если граф не является взвешенным, то под длиной пути понимается количество дуг, входящих в маршрут.

Если граф является взвешенным, т.е. каждой дуге (хi xj) приписан вес w (если вершины не соединены дугой, то вес считается равным бесконечности), то длиной пути является сумма весов всех дуг, входящих в этот путь.

Алгоритм Дейкстры позволяет определить кратчайший путь от вершины s до вершины t при условии, что веса всех дуг не отрицательны. На каждом шаге этого алгоритма каждая вершина графа xi имеет метку l(xj), которая может быть постоянной или временной.

Если метка l(хi) является временной, ее значение в дальнейшем может уменьшиться. Если1(хi) —постоянна, то она не изменится до конца работы алгоритма.

Кроме меток l(xi) с каждой вершиной графа связывается метка Q(xi), ее значение является номером вершины, предшествующей: вершине xi в кратчайшем пути. Основные шаги алгоритма Дейкстры:

1. Присвоить l(s)=0 и считать эту метку постоянной. Присвоить для всех остальных вершин xi l(xj)= и считать эти метки временными. Присвоить p=s, где р —вершина с наименьшей временной меткой.

2. Для всех вершин хi 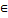Г(р), метки которых временны, изменить их в соответствии с правилом;

l(х i) = min(l(xi), l(р) + w(p, Xi)). Если метка вершины xi уменьшилась (l(p)+w(p, xj)< 1(х$)), то присвоить Q(хi)=р.

3. Если l(xj)= для всех вершин хi метки которых временны, то в исходном графе отсутствуют пути из вершины s b t. В противном случае, переход к шагу4.

4. Среди вершин с временными метками выбрать вершину хi метка которой минимальна, и считать эту метку постоянной::

1(х*) = min[l(xi;)]. Присвоить р=х*, меткуQ(p) считать постоянной.

5. Если p 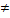t, то перейти к шагу 2, в противном случае — 1(р) — длина кратчайшего пути из s b t. Вершины, через которые проходит маршрут, восстанавливаются с помощью меток Q(xi): (s,..., Q(Q(t)), Q(t), t).

131.Постановка задач оптимального выбора. Обобщенная схема процесса оптимального выбора. Классификация задач оптимизации и методов их решения. Основные факторы, влияющие на эффективность оптимизационного

Процесса.

Постановка задачи оптимизации. Оптимизацией называется процедура определения в соответствии с установленными критериями наилучшего варианта из множества допустимых. Объектами оптимизации могут быть технич. произведённые, соц. эконом и др системы. Каждый объект характер-ся набором параметров, среди кот можно выделить входные и выходные параметры. Входные пар-ры дел-ся на управляемые и неуправляемые. Будем обозначать вектор вводимого параметра Х=(х1..хn). Различают задачи структурной и параметрической оптимизации. Структурная оптимизация связана с определением оптимальной структуры объекта, а параметрическая – с определением оптимальных параметров.

Решение задач оптимизации начинается с формулировки математической оптимиз модели, Она запис-ся след образом:

f(x)->max(min)

g(x)<(>.=)bj, i=l...m функциональные ограничения, которые являются некой функцией от варьируемых параметров.

х^min <х <х^max;, j=l...n прямые ограничения на варьируемые параметры

f(x)-это целевая функция, или критерий оптимальности.

Совокупность прямых и функциональных ограничений образует область допустимых решений оптимизационной задачи. Решение задач оптимизации заключается в определении таких значений варьируемых пар-ров. кот обеспечивали бы оптимальное значение целевой ф-ции и удовлетворялись в системе ограничений.

Классификация задач оптимизации,

1. В зависимости от количества управляемых параметров различают задачи одномерной и многомерной оптимизации;

2. В зависимости от числа критериев оптимальности различают задачи однокритериальной и многокритериальной оптимизации;

3. В зависимости от наличия ограничений различают задачи безусловной и условной оптимизации;

4. По виду целевой ф-ции и ограничений различают задачи линейной и нелинейной оптимизации. В задачах лин оптим-и целевая ф-ция и все ограничения линейны, в задач ах нелин-ой оптимизации хотя бы одна из ф-ций нелинейная;

5. По хар-ру изменения варьируемых пар-ров различают задачи непрерывной и дискретной оптимиз-и(в задачах непрерывной оптим-и пар-ры мен-ся непрерывно в заданных примерах, а в задачах дискретных — дискретные значения);