Требования, предъявляемые к математическим моделям, уровни моделирования

Математическая модель представляет собой формализованное описание сис-мы с помощью абстрактного языка, отражающего процесс функционирования. Для составления модели можно использовать любые математические средства. Бывают: аналитические, численные, имитационные.

Требования, предъявляемые к математическим моделям. К математ. моделям предъявляются следующие основные требования:

- универсальности;- точности;- адекватности; - экономичности.

Универсальность мат. модели характеризует полноту отражения в ней свойств реального объекта. Мат. модель отражает не все, а лишь некоторые свойства реального объекта.

Точность мат. модели оценивается степенью совпадения значений выходных параметров реального объекта и значений тех же параметров, рассчитанных с помощью модели.

Адекватность математической модели — это ее способность отражать заданные свойства объекта с погрешностью, не выше заданной.

Экономичность мат. модели характеризуется затратами вычислительных ресурсов на ее реализацию. Если работа с мат. моделью осуществляется вручную, то ее экономичность определяется затратами личного времени проектировщика. Если модель используется при автоматизированном проектировании, то затратами машинного времени и памяти компьютера.

К математическим моделям предъявляется и целый ряд других требований, среди которых следует выделить следующие:

Вычислимость, т.е. возможность ручного или с помощью ЭВМ исследования качественных и количественных закономерностей функционирования объекта (системы).

Модульность, т.е. соответствие конструкций модели структурным составляющим объекта (системы).

Алгоритмизируемость, т.е. возможность разработки соответствующе алгоритма и программы, реализующей математическую модель на ЭВМ. Наглядность, т.е. удобное визуальное восприятие модели.

 

177 оценка свойств математической модели технической системы

По спектру матрицы Якоби можно оценить устойчивость линейной динамической системы и характер переходных процессов. Понятие устойчивости системы связано со способностью ее возвращаться с определенной точностью в состояние равновесия после исчезновения внешних воздействий, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, а либо удаляется от него, либо совершает вокруг него колебания с недопустимо большими амплитудами.

Следует отметить, что большинство реальных физических систем нелинейные. Но на ранних стадиях проектирования часто применяют для их описания системы линейных дифференциальных уравнений, т. е. по существу осуществляют линеаризацию математической модели технической системы. Для нелинейных систем существует понятие устойчивости в малом и устойчивости в большом. При малых отклонениях от положения равновесия нелинейная система может быть устойчивой, а при больших — неустойчивой. Поэтому нельзя ограничиться анализом устойчивости линеаризованной системы. Устойчивость в большом может быть определена лишь на основе решения уравнений нелинейной математической модели. Обычно такой анализ выполняется на заключительной стадии проектирования, а на начальных стадиях ограничиваются анализом устойчивости линеаризованной системы по спектру матрицы Якоби.

Оценка устойчивости является одной из первостепенных задач проектирования. Если рассматриваемый вариант структуры технической системы не обладает устойчивостью, он не может быть использован для дальнейшей разработки конструкции.

Равновесный режим устойчивой технической системы, при котором все ее фазовые координаты v_i, i= 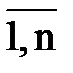остаются постоянными, устанавливается по истечении некоторого интервала времени после приложения внешних воздействий. При этом внешние воздействия должны быть постоянными и в дальнейшем не изменяться. Установившийся равновесный режим может быть нарушен вследствие изменения внешних управляющих или возмущающих воздействий, структуры технической системы (в системе с переменной структурой) или начальных условий (в процессе вычислительного эксперимента). В этом случае возникнет режим неустановившегося состояния системы, характеризуемый изменением ее фазовых координат во времени v_i(t). Неустановившееся состояние физической системы характеризуется избытком или недостатком энергии ее источника, необходимой для привода рабочих органов или передаваемой внешним потребителям, что приводит к изменению режима ее работы.

Определим условия, которым должна удовлетворять линеаризованная математическая модель, чтобы техническая система была устойчивой и имела затухающие переходные процессы. Систему из n уравнений первого порядка приведем к одному дифференциальному уравнению n-го порядка относительно некоторой фазовой переменной v:

 

 

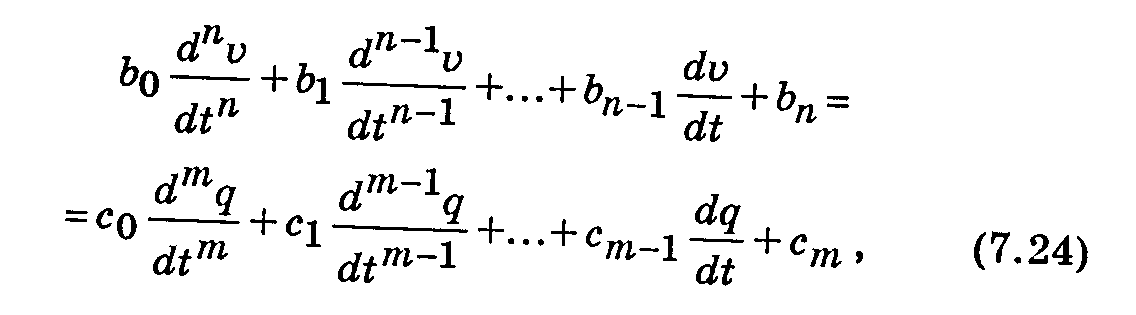
где q — одно из внешних воздействий на систему, изменяемое в переходном процессе.

Так как для линейной системы применим принцип суперпозиции, то можно получить решения v_j(q_j,t) для всех внешних воздействий q_j, j= 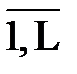, где L — количество внешних воздействий. Результирующее решение будет равно сумме всех составляющих решений. Поэтому будем рассматривать лишь одно внешнее воздействие q_j = q.

Запишем дифференциальное уравнение (7.24) в операторной форме:

 

(b₀pⁿ + b₁p^n-l +...+ b_n-1p + b_n)v(t) =

=(c₀p^m + c₁p^{m -1} +...+ c_m-1p +…+ c_m]q(t). (7.25)

 

где р = d/dt — оператор дифференцирования.

Решение этого неоднородного дифференциального уравнения представляет собой сумму двух решений — частного решения неоднородного уравнения и общего решения однородного уравнения (однородное уравнение получают из неоднородного, приравнивая нулю его правую часть). Первое слагаемое определяет вынужденную установившуюся составляющую v_в(t), второе — переходную составляющую v_п(t), характеризующую свободный переходный процесс исследуемой системы:

 

 

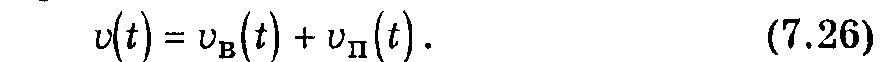
Техническая система будет устойчивой, если переходная составляющая с течением времени затухает, т. е. выполняется условие

 

 

Если с увеличением времени t переходный процесс расходится, т. е.

то техническая система будет неустойчивой.

Системы, в которых переходный процесс с течением времени не расходится и не затухает, называются находящимися на границе устойчивости.

Характер изменения переходной составляющей линейной технической системы зависит только от ее физических свойств, описываемых левой частью уравнения (7.25), т. е. однородным дифференциальным уравнением

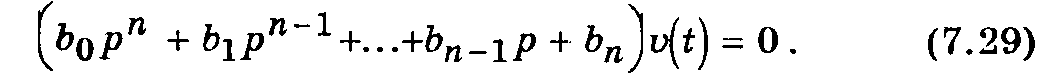
Поэтому свойства линейной системы изучают на основании анализа функции v_п(t), представляющей собой общее решение уравнения (7.28). Это решение ищут в виде

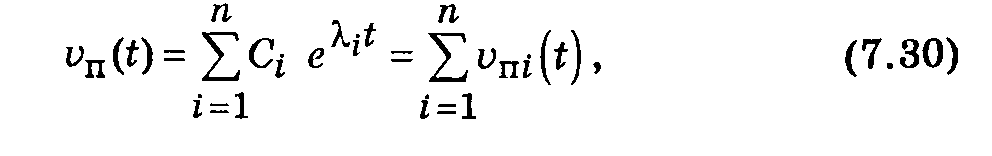
где С_i — постоянные интегрирования, определяемые из начальных условий; l_i — корни характеристического уравнения; v_пi(t) — слагаемое свободного переходного процесса, соответствующее корню l_i.

Характеристическое уравнение составляется непосредственно по виду однородного дифференциального уравнения (7.29)

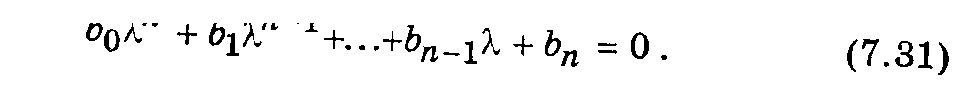
Характеристическое уравнение (7.31) является одновременно характеристическим полиномом матрицы Якоби системы линейных обыкновенных дифференциальных уравнений (7.2), а множество его корней l_i, i= 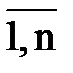составляет спектр матрицы Якоби. Количество корней n равно общему порядку системы уравнений (7.2).

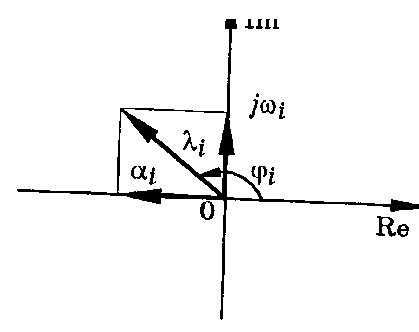
Среди множества корней характеристического полинома могут быть вещественные корни l_i = a_i, комплексные попарно-сопряженные l_i = a_i ± jw_i, мнимые l_i = ±jw_i, нулевые l_i = 0. Корни l_i представляют собой векторы, которые можно изобразить на комплексной плоскости. Модуль и аргумент вектора l_i находят по формулам:

 

 

 

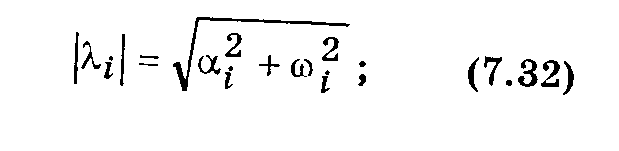
178 распределение вероятностей

При статистическом анализе технических систем используют различные теоретические распределения вероятностей случайных процессов (законы распределения). Для непрерывных случайных процессов наиболее часто употребляют нормальное распределение, распределение Пирсона, гамма-распределение, экспоненциальное распределение. Для дискретных случайных величин используют биномиальное распределение и распределение Пуассона.

Нормальное распределение (закон Гаусса) находит самое широкое практическое применение. Главная особенность, выделяющая нормальное распределение среди других законов, состоит в том, что оно является предельной формой многих распределений.

Одномерная плотность вероятности нормального распределения случайной величины Х определяется выражением

 

 

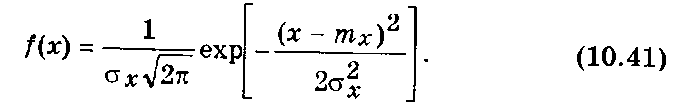
Из выражения (10.41) следует, что нормальное распределение полностью определяется двумя числовыми характеристиками: математическим ожиданием m_x и дисперсией 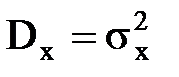. Функция распределения

 

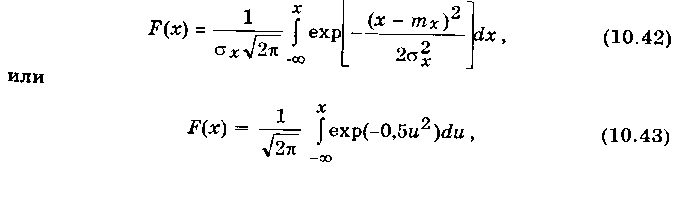где u — нормированное значение центрированной случайной величины, выраженное в долях s_x;

 

Функцию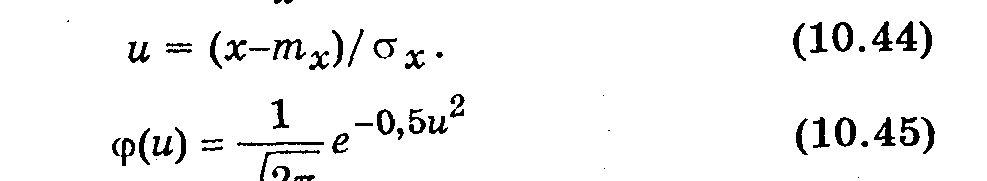

называют плотностью вероятности нормированного нормального распределения. Однако во всех случаях .

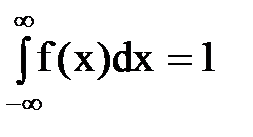Интегралы, входящие в формулы (10.42) и (10.43), не выражаются через элементарные функции. Поэтому для вычисления F(x) пользуются таблицами функции

 

 

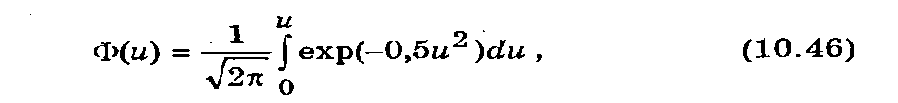
которая называется функцией Лапласа (интегралом вероятностей). Значения функции Лапласа Ф(u) приведены в табл. 1 приложения.

Определим вероятность попадания случайной величины Х в интервал
а <Х <b. В соответствии с (10.6) находим

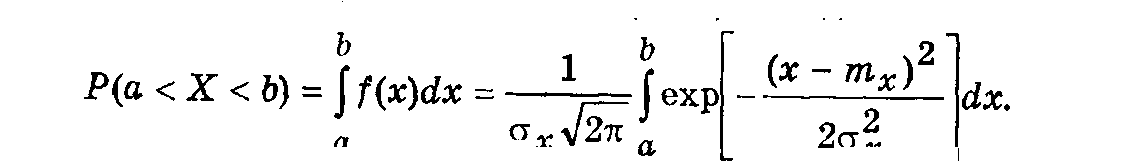
Если ввести нормированную переменную u согласно выражению (10.44), то Р(а < Х <b) = Ф(u₂) - Ф(u₁), (10.47)где u₁ = (а — m_x)/s _x; u₂ = (b — m_x)/s _x;.

Полученный результат отражает известное правило «трех сигм», которое гласит, что для нормально распределенной случайной величины отклонения ее от математического ожидания практически не превосходят 3s_х.

Логарифмически нормальное распределение описывает такие случайные величины, для которых нормально распределена не сама величина X, а ее логарифмы (десятичный или натуральный), т. е. Y = lgX (или Y = lnХ), причем 0 < Х < ¥. Плотность вероятности десятичного логарифма случайной величины определяется выражением

 

 

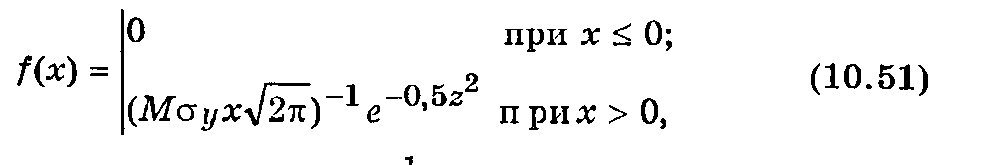
где z = (lgx — lgx₀)/s_y; М = (lge)^-1 = 2,303; е — основание натуральных логарифмов.

Среднее значение случайной величины и ее дисперсия вычисляются по формулам:

 

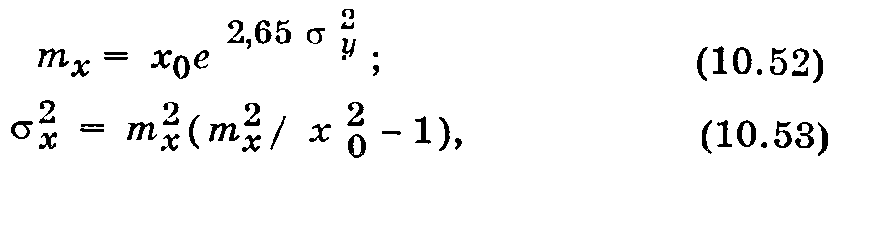
причем m_y = lgx₀.

Распределение (10.51) используется в теории надежности для описания времени безотказной работы технических объектов. При малых s_у (s_у < 0,1...0,13) распределение (10.51) близко к нормальному.

При Y = lnХ в приведенных формулах М = 1 и десятичные логарифмы заменяются натуральными.

Распределение Пирсона, находит широкое применение в математической статистике и теории надежности. Его используют для оценки согласованности экспериментальных распределений с теоретическими. Распределением Пирсона с k степенями свободы называют распределение суммы квадратов
c² = 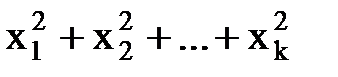, независимых случайных величин, каждая из которых имеет нормальное распределение с m_x = 0 и 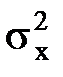= 1. Плотность вероят-ости распределения Пирсона

 

 

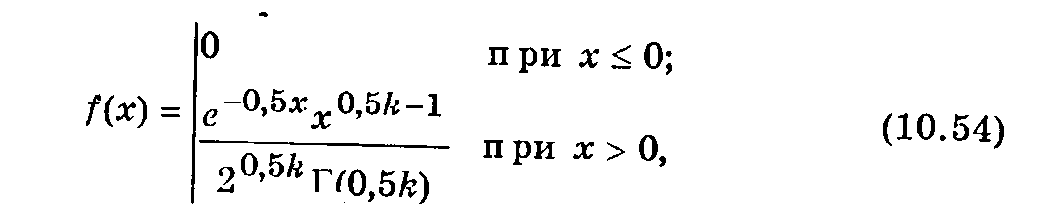
где Г(0,5k) — гамма-функция, значения которой приводятся к таблицах; k —значение случайной величины c₂.

Моменты распределения Пирсона: m_x k; 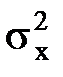2k а коэффициенты асимметрии и эксцесса А_x = 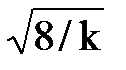; Е_x = 12/k.

 

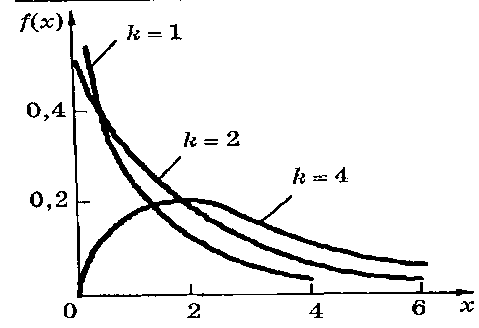
Рис. 10.8. Графики плотности вероятности распределения Пирсона

С увеличением k распределение c², приближается к нормальному (рис. 10.8).

Экспоненциальное распределение используется в теории надежности и теории массового обслуживания. Оно определяется одним параметром l, который называют интенсивностью потока событий. Плотность вероятности и функция распределения определяются выражениями:

 

 

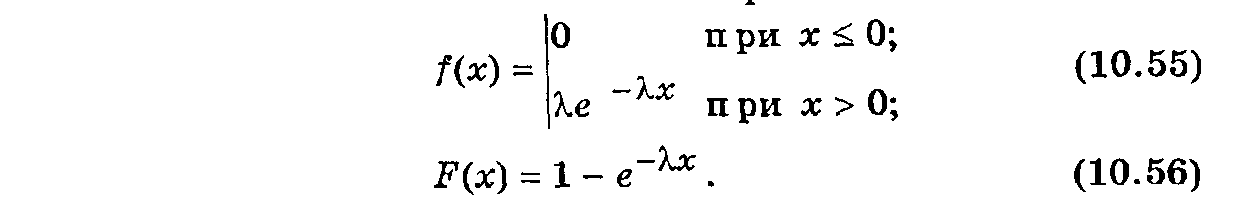
При простейшем потоке отказов значение е^-lx определяет вероятность безотказной работы в промежутке (0,х). Моменты экспоненциального распределения т_x = s_x =l^-1, а коэффициенты асимметрии и эксцесса А_x = 2; Е _x = 6. График функции f(x) показан на рис. 10.9.

Гамма-распределение представляет собой распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону. Плотность вероятности (рис. 10.10)

 

 

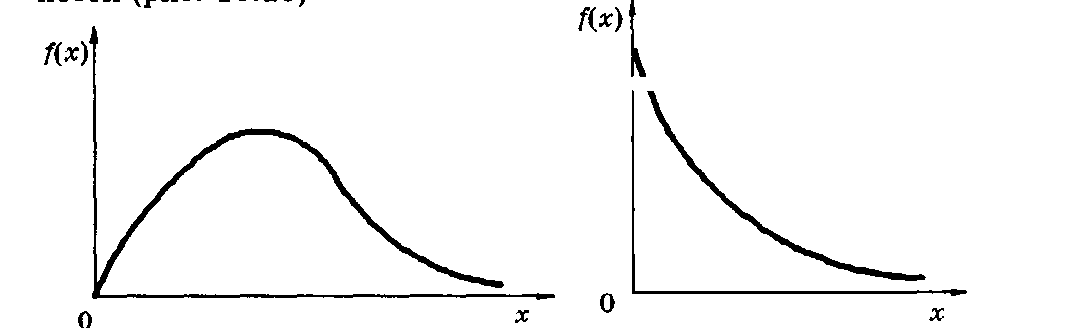
Рис. 10. 9. График плотности Рис. 10. 10. График плотности вероятности экспоненциального вероятности гамма-распределения распределения

 

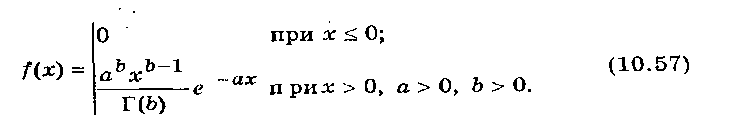
Постоянные а и b в выражении (10.57) являются параметрами гамма-распределения и определяют все его числовые характеристики: m _x = b/а; s _x = 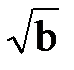; А _x = 2/ 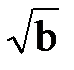; Е _x = 6/b. Если в выражении (10.57) положить 2b = k и а = 2, то получим распределение (10.54), а при b = 1 и а = l — распределение (10.55).

Биномиальное распределение используется для описания дискретных случайных величин. Вероятность того, что событие А осуществится ровно x раз при N испытаниях, определяется по формуле биномиального распределения:

 

 

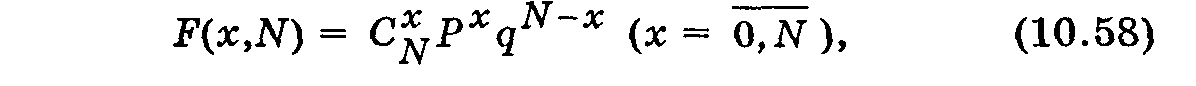
где q = 1-Р — вероятность неосуществления события А в каждом опыте; 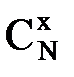— число сочетаний из N элементов по х элементов

 

 

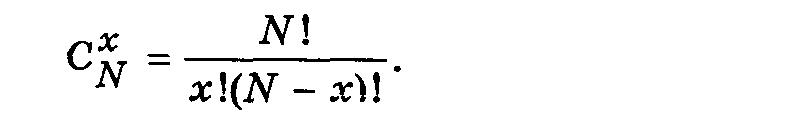
Математическое ожидание m_x = NP, дисперсия 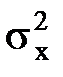= NPq. Распределение Пуассона является предельным для биномиального распределения. При неограниченном увеличении N и уменьшении Р так, что при этом NP =l= const, получим

 

 

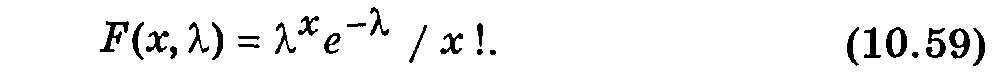
Величина l является параметром распределения Пуассона. Выражение (10.59) описывает распределение числа х случайных событий в каком-либо интервале времени, если можно считать, что вероятность наступления события за интервал Dt пропорциональна этому интервалу и события в разные моменты времени независимы. Математическое ожидание m_x и дисперсия 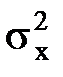распределения равны l. Значения функции F(x, l) приводятся в таблицах.

Равномерное распределение используют главным образом при моделировании случайных величин. На основе этого распределения составлены таблицы случайных чисел, используемые для решения разных практических задач: случайного взятия проб из каких-либо партий, проведения опытов в случайной последовательности и т.д. (см. табл. 7 приложения).

Вероятность попадания равномерно распределенной случайной величины Х в любые равные между собой интервалы, принадлежащие области возможных численных значении Х, одна и та же. Это означает, что плотность вероятности случайной величины Х постоянна и задается выражением

 

 

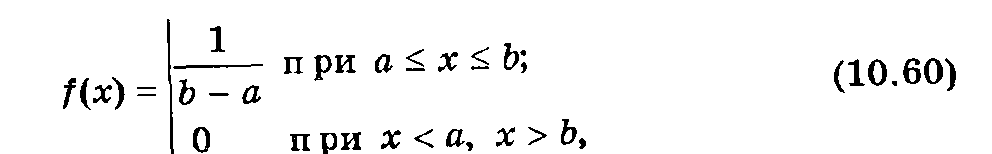
где а и b — произвольные вещественные числа, являющиеся границами области возможных значений X. Функция распределения

 

 

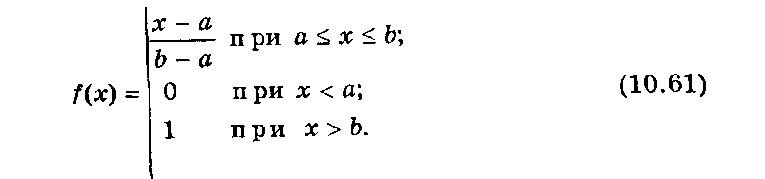
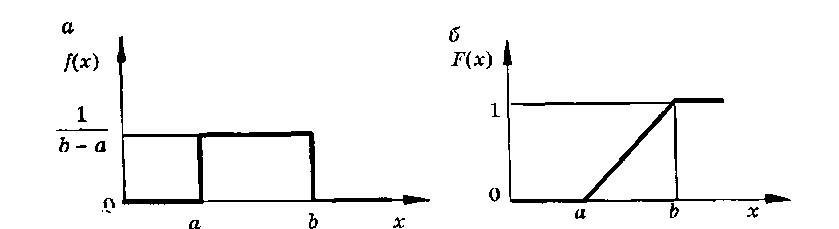
Рис. 10. 11. Графики плотности вероятности f(x) (а) и функции распределения F(x) (б) для равномерно распределенной случайной величины в интервале а < Х < b

 

Графики функций f(x) и F(x) приведены на рис. 10.11. Математическое ожидание и дисперсия равномерно распределенной случайной величины Х определяются по формулам:

 

 

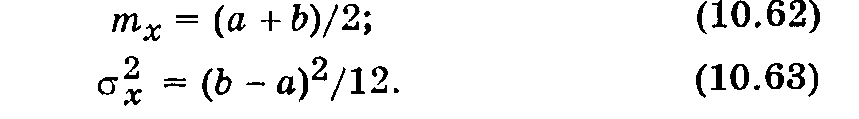
Обычно в теории и практических приложениях используют случайные числа, равномерно распределенные на интервале [0, 1]. В этом случае m_x = 1/2, 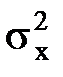= 1/12.