В предыдущем параграфе был рассмотрен симплекс-метод решения ЗЛП. Алгоритм симплекс-метода основан на последовательном улучшении (минимизации) целевой функции и построении базисного (опорного) решения (плана). Оптимальное решение достигается последовательным улучшением начального опорного плана за определенное число этапов (итераций). Переход к следующему опорному решению проводится на основе метода Жордана–Гаусса для систем линейных алгебраических уравнений. Направление перехода от одного базисного решения к другому выбирается на основе двух теорем (принципов оптимальности ЗЛП, теорема 5.1, теорема 5.2). Полученный опорный план на каждом шаге симплекс-метода проверяется на оптимальность. Процесс оканчивается за конечное число шагов. Причем на последнем шаге либо получается оптимальный опорный план и соответствующее ему оптимальное значение целевой функции (теорема 5.1), либо выявляется неразрешимость задачи (конечного оптимума нет).
Оказывается, что все вычисления по симплекс-методу удобно производить в так называемых симплекс-таблицах.
Как и в предыдущем параграфе, рассмотрим ЗЛП в допустимом виде
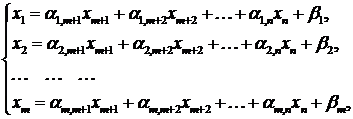 (6.1)
(6.1)
где базисные переменные 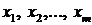 выражены через свободные переменные
выражены через свободные переменные 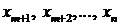 , причем
, причем 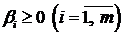 . Целевая функция имеет вид
. Целевая функция имеет вид
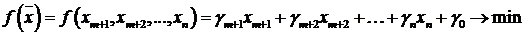 . (6.2)
. (6.2)
Приведем ЗЛП (6.1) – (6.2) к каноническому виду
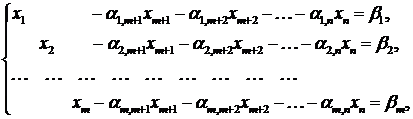 (6.3)
(6.3)
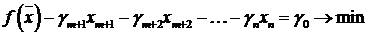 . (6.4)
. (6.4)
Рассмотрим алгоритм решения ЗЛП, используя результаты предыдущего параграфа (теоремы 5.1, 5.2). В целях наглядности рассмотрим ЗЛП
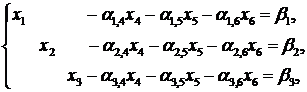 (6.3′)
(6.3′)
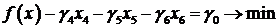 , (6.4′)
, (6.4′)
в которой три базисные переменные  и три свободные переменные
и три свободные переменные 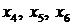 , причем
, причем 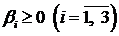 .
.
Составим начальную симплекс-таблицу (табл. 6.1). В столбце БП выписываем базисные переменные  , в столбце СЧ – коэффициенты
, в столбце СЧ – коэффициенты 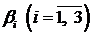 в правой части системы ограничений (6.3′). В следующих столбцах выписываются коэффициенты при переменных в левой части системы (6.3′). Последняя строка таблицы составляется по коэффициентам при переменных в целевой функции (6.4′).
в правой части системы ограничений (6.3′). В следующих столбцах выписываются коэффициенты при переменных в левой части системы (6.3′). Последняя строка таблицы составляется по коэффициентам при переменных в целевой функции (6.4′).
Табл. 6.1
| БП | СЧ | 
| 
| 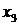
| 
| 
| 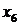
|

| 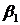
| 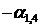
| 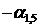
| 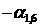
| |||

| 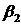
| 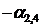
| 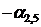
| 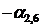
| |||
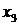
| 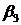
| 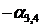
| 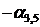
| 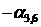
| |||
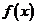
| 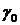
| 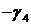
| 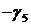
| 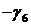
|
По табл. 6.1 построим начальный: 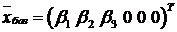 (значения свободных переменных
(значения свободных переменных 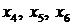 равны нулю); соответственно значение целевой функции на базисном решении
равны нулю); соответственно значение целевой функции на базисном решении 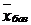 равно
равно 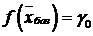 .
.
Проверим построенное базисное решение 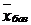 на оптимальность. Возникают три случая:
на оптимальность. Возникают три случая:
Случай 1. Пусть в последней строке симплекс-таблицы все коэффициенты при свободных переменных 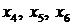 неположительны:
неположительны:
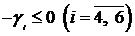 .
.
Это условие равносильно тому, что 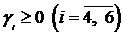 . Тогда согласно теореме 5.1 базисное решение
. Тогда согласно теореме 5.1 базисное решение 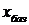 является оптимальным:
является оптимальным:
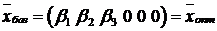 ,
, 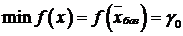 .
.
Случай 2. Пусть в последней строке симплекс-таблицы среди коэффициентов 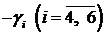 есть положительный коэффициент (предположим для определенности:
есть положительный коэффициент (предположим для определенности: 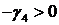 ), а все коэффициенты при соответствующей свободной переменной отрицательные (в нашем случае все коэффициенты
), а все коэффициенты при соответствующей свободной переменной отрицательные (в нашем случае все коэффициенты 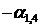 ,
, 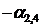 ,
, 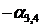 при соответствующей свободной переменной
при соответствующей свободной переменной  отрицательны). Это условие равносильно тому, что
отрицательны). Это условие равносильно тому, что
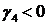 ,
, 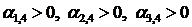 .
.
Тогда согласно теореме 5.2, ЗЛП не имеет оптимального решения.
Случай 3. Пусть в последней строке симплекс-таблицы среди коэффициентов 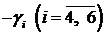 есть положительный, и при соответствующей свободной переменной в системе ограничений также имеется положительный коэффициент. Предположим для определенности, что
есть положительный, и при соответствующей свободной переменной в системе ограничений также имеется положительный коэффициент. Предположим для определенности, что 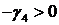 , и при соответствующей свободной переменной
, и при соответствующей свободной переменной  в системе ограничений среди
в системе ограничений среди 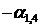 ,
, 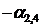 ,
, 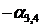 имеется положительный коэффициент. При этом столбец коэффициентов при переменной
имеется положительный коэффициент. При этом столбец коэффициентов при переменной  в таблице называется разрешающим столбцом (выделяем его в таблице вертикальной стрелкой
в таблице называется разрешающим столбцом (выделяем его в таблице вертикальной стрелкой 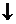 ). Согласно предыдущему параграфу, необходимо изменить базис переменных. Составим вспомогательное число
). Согласно предыдущему параграфу, необходимо изменить базис переменных. Составим вспомогательное число
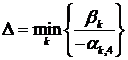 ,
,
где индекс  принимает те значения от 1 до 3, при которых
принимает те значения от 1 до 3, при которых 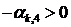 . Предположим для определенности, что
. Предположим для определенности, что 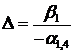 . Тогда число
. Тогда число 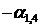 называется разрешающим элементом (выделен в табл. 6.2 в прямоугольник, строка коэффициентов при переменной
называется разрешающим элементом (выделен в табл. 6.2 в прямоугольник, строка коэффициентов при переменной  называется разрешающей строкой).
называется разрешающей строкой).
Табл. 6.2
| БП | СЧ | 
| 
| 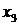
| 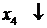
| 
| 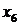
| Преобразования |
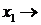
| 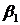
| 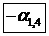
| 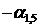
| 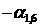
|  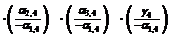
| |||

| 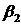
| 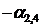
| 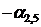
| 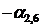
|  
| |||
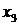
| 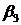
| 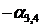
| 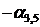
| 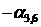
| ||||
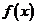
| 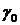
| 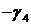
| 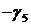
| 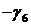
|
Согласно симплекс-методу, необходимо изменить базис переменных: переменную  вывести из базиса, а
вывести из базиса, а  ввести в базис. Для этого составляется новая симплекс-таблица (табл. 6.3) по следующему правилу:
ввести в базис. Для этого составляется новая симплекс-таблица (табл. 6.3) по следующему правилу:
1) Базисными переменными являются 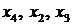 , свободными – переменные
, свободными – переменные 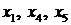 (переменная
(переменная  сменила переменную
сменила переменную  в базисе);
в базисе);
2) Разрешающая строка (в данном случае строка коэффициентов при переменной  ) делится на разрешающий элемент (в нашем случае на
) делится на разрешающий элемент (в нашем случае на 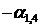 ). Полученная строка записывается в строку соответствующей новой базисной переменной;
). Полученная строка записывается в строку соответствующей новой базисной переменной;
3) В разрешающем столбце таблицы 6.2 (в столбце коэффициентов при  ) необходимо получить нули. Для этого применяем элементарные преобразования над строками таблицы 6.2. Полученные результаты записываем в соответствующие строки табл. 6.3.
) необходимо получить нули. Для этого применяем элементарные преобразования над строками таблицы 6.2. Полученные результаты записываем в соответствующие строки табл. 6.3.
Табл. 6.3
| БП | СЧ | 
| 
| 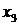
| 
| 
| 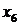
|

| 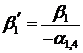
| 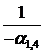
| 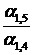
| 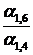
| |||

| 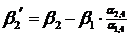
| 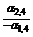
| 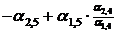
| 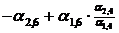
| |||
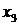
| 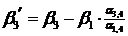
| 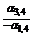
| 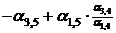
| 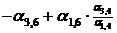
| |||
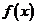
| 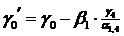
| 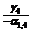
| 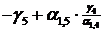
| 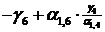
|
Покажем, что в табл. 6.3 коэффициенты 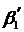 ,
, 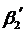 ,
, 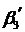 неотрицательны. Действительно,
неотрицательны. Действительно, 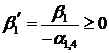 (так как по
(так как по 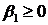 ,
, 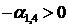 ).
).
Далее, если даже коэффициент 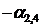 отрицательный, то в силу того, что
отрицательный, то в силу того, что 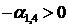 :
:
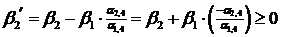 .
.
Если же коэффициент 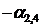 положительный, то в силу выбора разрешающего элемента имеем
положительный, то в силу выбора разрешающего элемента имеем
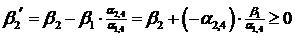 .
.
Итак, в любом случае коэффициент 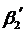 неотрицательный. Аналогично показывается, что коэффициент
неотрицательный. Аналогично показывается, что коэффициент 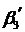 неотрицательный.
неотрицательный.
Это показывает, что вектор-столбец 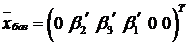 , полученный при нулевых значениях свободных переменных, является допустимым решением ЗЛП.
, полученный при нулевых значениях свободных переменных, является допустимым решением ЗЛП.
Значение целевой функции на базисном решении 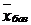 равно
равно
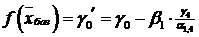 .
.
Так как по условию 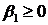 ,
, 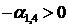 ,
, 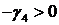 , то
, то 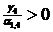 , а значит,
, а значит,
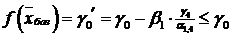 ,
,
то есть в процессе смены базиса целевая функция ЗЛП уменьшилась на значение 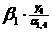 , что является оправданием шага симплекс-метода.
, что является оправданием шага симплекс-метода.
Пользуясь таблицей 6.3, далее необходимо вновь проверить базисное решение 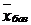 на оптимальность (проверить возможность возникновения одного из трех описанных случаев).
на оптимальность (проверить возможность возникновения одного из трех описанных случаев).
Пример 6.1. Решить ЗЛП при помощи симплекс-таблиц.
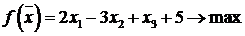
 ,
,
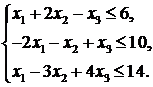
Решение. 1) Приведем ЗЛП к каноническому виду. Введем в систему ограничений балансовые переменные 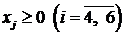 . Так как
. Так как 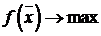 , то введем функцию
, то введем функцию
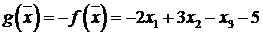 ,
,
сведя задачу к поиску минимума функции 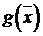 :
: 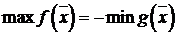 .
.
Получили следующую ЗЛП канонического вида
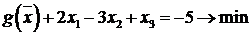
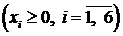 ,
,
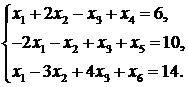
2) Для полученной ЗЛП базис переменных 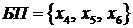 . Составим базисное решение
. Составим базисное решение 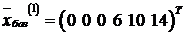 ,
, 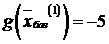 . Получаем симплекс-таблицу (табл. 6.4).
. Получаем симплекс-таблицу (табл. 6.4).
Табл. 6.4
| БП | СЧ | 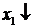
| 
| 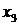
| 
| 
| 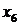
| Преобразования |
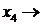
| 
| –1 |    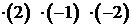
| |||||

| –2 | –1 | ||||||
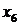
| –3 | |||||||
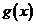
| – 5 | –3 |
Проверяем базисное решение 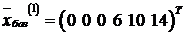 на оптимальность. В полученной табл. 6.4 в последней строке коэффициентов при переменных
на оптимальность. В полученной табл. 6.4 в последней строке коэффициентов при переменных 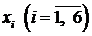 присутствует положительный коэффициент (
присутствует положительный коэффициент (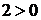 ). Столбец
). Столбец  является разрешающим (отмечаем
является разрешающим (отмечаем 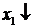 ). Составляем число
). Составляем число
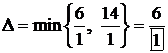 ,
,
откуда следует, что число 1 – знаменатель первой (наименьшей) дроби является разрешающим элементом (он выделен в табл. 6.4 в прямоугольнике, строка коэффициентов при переменной  является разрешающей строкой). Производим смену базиса:
является разрешающей строкой). Производим смену базиса: 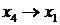 .
.
3) Составляем следующую симплекс-таблицу. Для этого делим  -строку табл. 6.4 на разрешающий элемент
-строку табл. 6.4 на разрешающий элемент  и при помощи элементарных преобразований обнуляем элементы, стоящие под разрешающим элементом. Получаем табл. 6.5.
и при помощи элементарных преобразований обнуляем элементы, стоящие под разрешающим элементом. Получаем табл. 6.5.
Табл. 6.5
| БП | СЧ | 
| 
| 
| 
| 
| 
| Преобразования |

| – 1 | 
| ||||||

| – 1 | 
| ||||||
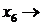
| – 5 | 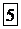
| – 1 |  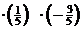
| ||||
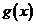
| – 17 | – 7 | – 2 |
Переменные 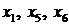 образуют базис переменных:
образуют базис переменных: 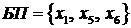 . Составим базисное решение
. Составим базисное решение 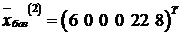 ,
, 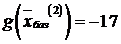 . Как видно,
. Как видно, 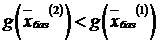 , то есть в результате шага симплекс-метода целевая функция
, то есть в результате шага симплекс-метода целевая функция 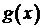 уменьшила свое значение на 12.
уменьшила свое значение на 12.
4) Проверим базисное решение 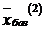 на оптимальность. Как видно из табл. 6.5, разрешающим столбцом является
на оптимальность. Как видно из табл. 6.5, разрешающим столбцом является 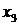 -столбец, разрешающим элементом – элемент 5. Происходит смена базиса:
-столбец, разрешающим элементом – элемент 5. Происходит смена базиса: 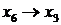 . В результате шага симплекс-метода получаем таблицу 6.6.
. В результате шага симплекс-метода получаем таблицу 6.6.
Табл. 6.6
| БП | СЧ | 
| 
| 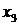
| 
| 
| 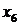
|

| 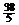
| 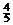
| 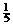
| ||||

| 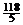
| 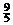
| 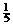
| ||||
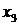
| 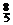
| – 1 | – 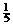
| 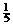
| |||
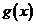
| – 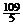
| – 4 | – 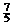
| 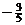
|
Базисное решение 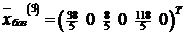 . При этом
. При этом 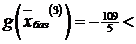
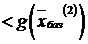 . Проверяя решение
. Проверяя решение 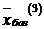 на оптимальность, замечаем, что в последней строке табл. 6.6, нет ни одного положительного числа. Согласно критерию оптимальности, базисное решение
на оптимальность, замечаем, что в последней строке табл. 6.6, нет ни одного положительного числа. Согласно критерию оптимальности, базисное решение 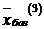 является оптимальным:
является оптимальным:
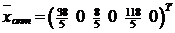 ,
, 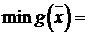
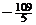 .
.
Возвращаясь к исходной задаче, записываем ответ:
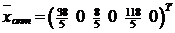 ,
, 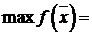
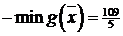 .
.
 2018-01-21
2018-01-21 1366
1366
