В основе теории двойственности лежат основные теоремы. Рассмотрим для определенности симметрическую пару ДЗЛП. Пусть прямая задача записана в следующем матричном виде
 ,
,  ,
,  , (9.1)
, (9.1)
где  – вектор-столбец коэффициентов целевой функции,
– вектор-столбец коэффициентов целевой функции,  – вектор-столбец управляющих переменных (
– вектор-столбец управляющих переменных ( ,
,  ),
),  – матрица коэффициентов при управляющих переменных,
– матрица коэффициентов при управляющих переменных,  – вектор-столбец свободных членов.
– вектор-столбец свободных членов.
Соответствующая ДЗЛП к прямой задаче (9.1) имеет вид
 ,
, 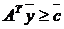 ,
,  , (9.2)
, (9.2)
где  – вектор-столбец управляющих переменных двойственной задачи (
– вектор-столбец управляющих переменных двойственной задачи ( ,
,  ).
).
Лемма 9.1 (основное неравенство теории двойственности).Для любых допустимых решений  и
и  пары взаимно двойственных задач (9.1), (9.2) справедливо неравенство
пары взаимно двойственных задач (9.1), (9.2) справедливо неравенство
 . (9.3)
. (9.3)
□ Пусть  ,
,  – допустимые решения задач (9.1), (9.2) соответственно. Умножим систему ограничений прямой задачи на вектор-столбец
– допустимые решения задач (9.1), (9.2) соответственно. Умножим систему ограничений прямой задачи на вектор-столбец  слева:
слева:

 .
.
Умножим систему ограничений двойственной задачи на вектор-столбец  справа:
справа:
 .
.
Тогда получим  , то есть для допустимых решений
, то есть для допустимых решений  и
и  задач (9.1) и (9.2) соответственно выполняется неравенство (9.3). ■
задач (9.1) и (9.2) соответственно выполняется неравенство (9.3). ■
Лемма 9.2. Если для допустимых решений  и
и  пары взаимно двойственных задач (9.1), (9.2) выполняется равенство
пары взаимно двойственных задач (9.1), (9.2) выполняется равенство 
 , то
, то
 и
и  являются оптимальными решениями соответствующих задач.
являются оптимальными решениями соответствующих задач.
□ В силу неравенства (9.3) для любого допустимого решения  задачи (9.1) выполняется неравенство
задачи (9.1) выполняется неравенство  , то есть
, то есть  . Это означает, что
. Это означает, что  , то есть
, то есть  является оптимальным решением задачи (9.1). Аналогично показывается, что
является оптимальным решением задачи (9.1). Аналогично показывается, что  является оптимальным решением задачи (9.2). ■
является оптимальным решением задачи (9.2). ■
Теорема 9.1 ( первая теорема двойственности ). Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций совпадают:  , или
, или  . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива (а значит, задача не имеет оптимального решения).
. Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива (а значит, задача не имеет оптимального решения).
Теорема 9.2 ( вторая теорема двойственности, теорема равновесия ). Пусть 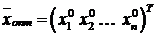 ,
,  есть оптимальные решения задач (9.1) и (9.2) соответственно. Тогда для векторов
есть оптимальные решения задач (9.1) и (9.2) соответственно. Тогда для векторов  ,
,  выполняются равенства
выполняются равенства
 (
( ) (9.4)
) (9.4)
 (
( ). (9.5)
). (9.5)
□ Пусть 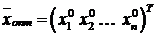 ,
,  есть оптимальные решения задач (9.1) и (9.2) соответственно. При этом согласно теореме 9.1
есть оптимальные решения задач (9.1) и (9.2) соответственно. При этом согласно теореме 9.1  . Умножим неравенство
. Умножим неравенство  слева на вектор
слева на вектор  :
:
 .
.
Умножим неравенство  справа на вектор-столбец
справа на вектор-столбец  :
:
 .
.
Так как  , то
, то  . Тогда из доказанного выше получим
. Тогда из доказанного выше получим
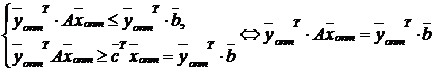 .
.
Итак,  . Расписывая покоординатно это равенство, получим равенства (9.4). Аналогично доказывается справедливость равенств (9.5). ■
. Расписывая покоординатно это равенство, получим равенства (9.4). Аналогично доказывается справедливость равенств (9.5). ■
Равенства (9.4) и (9.5) называются условиями дополняющей нежесткости. Из них следует:
1) если какое-либо неравенство системы ограничений одной из задач не обращается в строгое равенство оптимальным решением этой задачи, то соответствующая компонента оптимального решения двойственной задачи должна равняться нулю;
2) если какая-либо компонента одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным решением должно обращаться в строгое равенство, то есть
если  , то
, то  ; если
; если  , то
, то  ; (9.6)
; (9.6)
если  , то
, то  ; если
; если 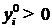 , то
, то  . (9.7)
. (9.7)
Теоремы 9.1 и 9.2 позволяют найти оптимальное решение одной из пары задач по решению другой.
Пример 9.1. Найти оптимальное решение ДЗЛП для прямой ЗЛП

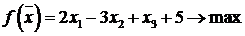
 ,
,
учитывая, что  ,
,  .
.
Решение. Соответствующая ДЗЛП имеет вид


 .
.
Воспользуемся равенствами (9.6): так как  , то первое ограничение в системе неравенств ДЗЛП выполняется как равенство:
, то первое ограничение в системе неравенств ДЗЛП выполняется как равенство:
 .
.
Аналогично, так как  , то
, то
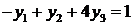 .
.
Так как  , то второе ограничение в системе неравенств ДЗЛП выполняется как строгое неравенство:
, то второе ограничение в системе неравенств ДЗЛП выполняется как строгое неравенство:
 .
.
Итак, имеем следующую систему для определения оптимального решения  ДЗЛП:
ДЗЛП:
 (9.8)
(9.8)
Воспользуемся теперь равенствами (9.7). Подставим компоненты оптимального решения  в систему ограничений прямой задачи:
в систему ограничений прямой задачи:

В силу того, что  , система (9.8) принимает вид
, система (9.8) принимает вид

Решая последнюю систему, получим  . Тогда вектор-столбец оптимального решения имеет вид
. Тогда вектор-столбец оптимального решения имеет вид  . При этом
. При этом
 .
.
Пример 9.2. Найти оптимальное решение ДЗЛП для прямой ЗЛП


 ,
,
учитывая, что  ,
,  .
.
Решение. Соответствующая ДЗЛП имеет вид


 .
.
Так как  ,
,  ,
,  , то воспользовавшись равенствами (9.6), получим систему для определения оптимального решения ДЗЛП:
, то воспользовавшись равенствами (9.6), получим систему для определения оптимального решения ДЗЛП:

Воспользовавшись равенствами (9.7), получим:  .
.
Согласно первой теоремой теории двойственности, имеем равенство
 .
.
Следовательно,  , то есть
, то есть
 .
.
Получаем систему для определения оптимального решения  ДЗЛП:
ДЗЛП:
 (9.9)
(9.9)
Решая из системы (9.9) первые три уравнения, получим структуру оптимального решения  ДЗЛП:
ДЗЛП:
 ,
,
где  . Используя неравенство в системе (9.9), получим
. Используя неравенство в системе (9.9), получим
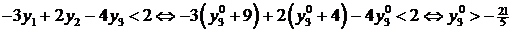 .
.
Учитывая тот факт, что  , неравенство
, неравенство  выполняется.
выполняется.
В результате заключаем, что ДЗЛП имеет бесконечное множество оптимальных решений (ДЗЛП имеет альтернативный оптимум)
 ,
,  .
.
 2018-01-21
2018-01-21 777
777








