(М -метод решения ЗЛП)
В предыдущем параграфе был описан алгоритм решения ЗЛП симплекс-методом. В качестве необходимого условия для решения ЗЛП симплекс-методом требовалось, чтобы система ограничений имела допустимый вид. В одних задачах такой базис усматривается непосредственно (см. например, пример 6.1). В других же задачах допустимый базис переменных приходится искать (перебирая различные варианты).
Наиболее общим методом нахождения допустимого базиса и соответственно решением ЗЛП является метод искусственного базиса (М-метод). М -метод применяется в тех случаях, когда затруднительно найти первоначальный допустимый базис переменных исходной ЗЛП, записанной в канонической форме. Пусть ЗЛПимеет канонический вид
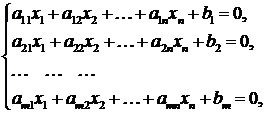 (7.1)
(7.1)
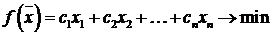 , (7.2)
, (7.2)
где  ,
, 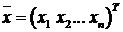 , причем
, причем 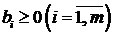 (этого условия легко можно добиться путем умножения
(этого условия легко можно добиться путем умножения  -го уравнения на число
-го уравнения на число  , если коэффициент
, если коэффициент 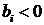 ). Наряду с ЗЛП (7.1) – (7.2) рассмотрим ЗЛП
). Наряду с ЗЛП (7.1) – (7.2) рассмотрим ЗЛП
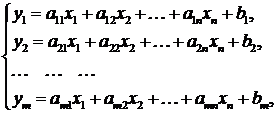 (7.3)
(7.3)
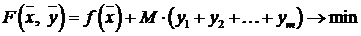 , (7.4)
, (7.4)
где 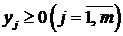 ,
,  ,
, 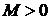 ,
, 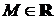 .
.
Определение 7.1. ЗЛП (7.3) – (7.4) будем называть М-задачей. Неизвестными в М -задаче являются 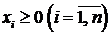 ,
, 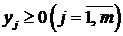 . Переменные
. Переменные 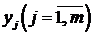 принято называть искусственными переменными, а вектор
принято называть искусственными переменными, а вектор  – вектор-столбцом искусственных переменных.
– вектор-столбцом искусственных переменных.
Так как в системе (7.3) 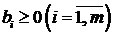 , то она имеет допустимый вид с допустимым базисом из искусственных переменных
, то она имеет допустимый вид с допустимым базисом из искусственных переменных 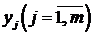 . Для решения М -задачи (7.3) – (7.4) можно воспользоваться симплекс-методом.
. Для решения М -задачи (7.3) – (7.4) можно воспользоваться симплекс-методом.
Замечание 7.1. В систему ограничений (7.3) мы ввели 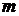 искусственных переменных
искусственных переменных 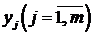 . Однако на практике при решении ЗЛП М -методом искусственных переменных может понадобиться меньше, чем количество
. Однако на практике при решении ЗЛП М -методом искусственных переменных может понадобиться меньше, чем количество 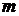 ограничений (см. пример 7.1).
ограничений (см. пример 7.1).
Следующие теоремы устанавливают связь между решениями исходной задачи (7.1) – (7.2) и соответствующей М -задачи (7.3) – (7.4).
Теорема 7.1. Пусть набор 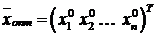 ,
,  есть оптимальное решение М -задачи (7.3) – (7.4) при каком-то значении
есть оптимальное решение М -задачи (7.3) – (7.4) при каком-то значении 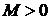 . Если при этом все значения
. Если при этом все значения 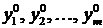 искусственных переменных равны нулю, то вектор
искусственных переменных равны нулю, то вектор 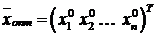 является оптимальным решением исходной задачи (7.1) – (7.2).
является оптимальным решением исходной задачи (7.1) – (7.2).
□ Пусть 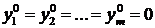 ,
, 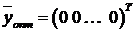 . Тогда значения
. Тогда значения 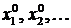
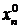 удовлетворяют системе ограничений (7.1). Предположим, что вектор
удовлетворяют системе ограничений (7.1). Предположим, что вектор 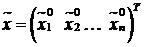 есть какое-нибудь другое решение системы (7.1). Покажем, что
есть какое-нибудь другое решение системы (7.1). Покажем, что 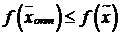 (этим будет показано, что
(этим будет показано, что 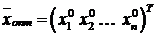 есть оптимальное решение ЗЛП (7.1) – (7.2)). Дополнив значения
есть оптимальное решение ЗЛП (7.1) – (7.2)). Дополнив значения 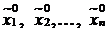 числами
числами 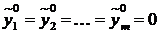 , получим, что вектор
, получим, что вектор
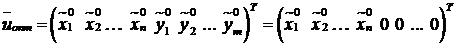
удовлетворяет системе (7.3). Ввиду оптимальности вектора  имеем
имеем
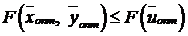 .
.
Учитывая, что 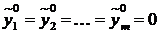 , находим
, находим
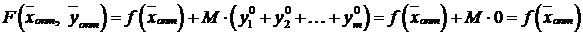 ,
,
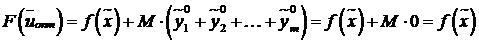 .
.
Тогда, так как 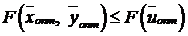 , то
, то 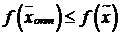 .
.
Заметим, что так как 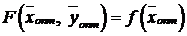 , то
, то
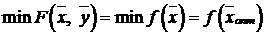 ■
■
Согласно теореме 7.1, если при решении М -задачи симплекс-методом получена симплекс-таблица, дающая оптимальное решение, причем в ней все искусственные переменные являются свободными (их значения равны нулю), то, отбросив столбцы для этих переменных, получим симплекс-таблицу, дающую оптимальное решение исходной задачи. Тогда, чтобы получить оптимальное решение исходной ЗЛП, необходимо на каждом шаге симплекс-метода стараться выводить искусственные переменные из базиса.
Теорема 7.2. Пусть набор 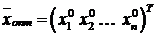 ,
,  есть оптимальное решение М -задачи (7.3) – (7.4) при всех значениях
есть оптимальное решение М -задачи (7.3) – (7.4) при всех значениях 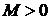 . Если при этом хотя бы одно из значений
. Если при этом хотя бы одно из значений 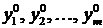 искусственных переменных отлично от нуля, то вектор система ограничений (7.1) несовместна (ЗЛП (7.1) – (7.2) не имеет допустимого решения).
искусственных переменных отлично от нуля, то вектор система ограничений (7.1) несовместна (ЗЛП (7.1) – (7.2) не имеет допустимого решения).
□ Доказательство проведем методом от противного. Предположим, что система (7.1) совместна и имеет допустимое (не обязательно оптимальное) решение 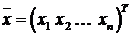 . Тогда вектор
. Тогда вектор 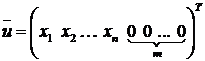 является решением системы ограничений (7.3). Так как набор
является решением системы ограничений (7.3). Так как набор  ,
,  является оптимальным решением М -задачи (7.3) – (7.4), то
является оптимальным решением М -задачи (7.3) – (7.4), то
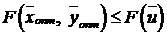 ,
,
что равносильно неравенству
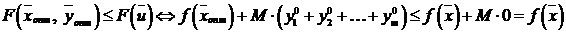 .
.
Итак, при всех значениях 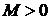 получили неравенство
получили неравенство
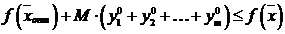 . (7.5)
. (7.5)
Так как среди значений 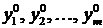 существует хотя бы одно положительное, то число
существует хотя бы одно положительное, то число 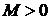 можно выбрать таким большим, что неравенство (7.5) не выполнится. Полученное противоречие доказывает теорему. ■
можно выбрать таким большим, что неравенство (7.5) не выполнится. Полученное противоречие доказывает теорему. ■
Согласно теореме 7.2, если при решении М -задачи получена симплекс-таблица, дающая при всех достаточно больших значениях 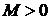 оптимальное решение, и в этой таблице хотя бы одна искусственная переменная осталась в базисе (ее значение положительно), то исходная ЗЛП не имеет оптимального решения.
оптимальное решение, и в этой таблице хотя бы одна искусственная переменная осталась в базисе (ее значение положительно), то исходная ЗЛП не имеет оптимального решения.
Теорема 7.3. Если М -задача (7.3) – (7.4) не имеет оптимального решения (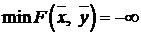 ), то ЗЛП (7.1) – (7.2) также не имеет оптимального решения (либо
), то ЗЛП (7.1) – (7.2) также не имеет оптимального решения (либо 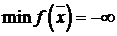 , либо система (7.1) несовместна).
, либо система (7.1) несовместна).
Пример 7.1. Решить М -методом ЗЛП
 ,
,
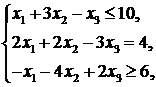
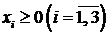 .
.
Решение. Приведем ЗЛП к каноническому виду и составим для ЗЛП соответствующую М -задачу. Для этого в первое и третье ограничения системы сначала введем балансовые переменные 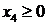 ,
, 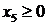 (целевая функция
(целевая функция  при этом не изменится):
при этом не изменится):
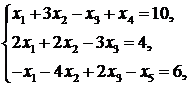
Переменная  войдет в базис, так как она встречается только один раз в системе ограничений и перед ней стоит положительный знак.
войдет в базис, так как она встречается только один раз в системе ограничений и перед ней стоит положительный знак.
Для получения допустимого базиса переменных во второе и третье уравнения последней системы введем искусственные переменные 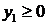 ,
, 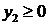 . В результате получим М -задачу (
. В результате получим М -задачу (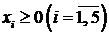 ,
, 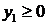 ,
, 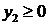 ) с допустимым базисом
) с допустимым базисом 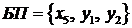 , системой ограничений
, системой ограничений
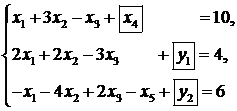 (7.6)
(7.6)
и целевой функцией
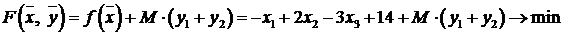 .
.
Упростим целевую функцию, которая в итоге должна зависеть от свободных переменных. Выражаем из системы (7.6) переменные 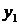 ,
, 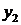 :
:
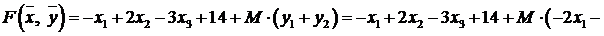
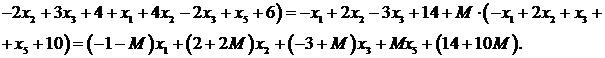
Итак, целевая функция 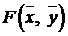 М -задачи имеет вид
М -задачи имеет вид
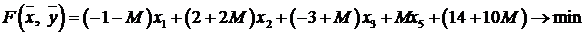 .
.
Приведем целевую функцию к каноническому виду:
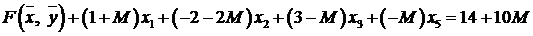 . (7.7)
. (7.7)
По системе ограничений (7.6) и целевой функции (7.7) построим начальную симплекс-таблицу (табл. 7.1).
Табл. 7.1
| БП | СЧ | 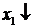 |  | 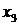 |  |  | 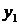 | 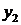 | Преобразования |
 | – 1 |   | |||||||
 |  | – 3 |   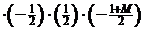 | ||||||
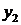 | – 1 | – 4 | – 1 | ||||||
 | 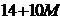 | 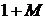 | 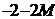 | 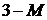 | 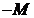 |  |
Базисное решение имеет вид
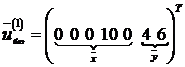 .
.
Проверим базисное решение 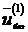 на оптимальность. В качестве разрешающего столбца выберем
на оптимальность. В качестве разрешающего столбца выберем  -столбец, так как при
-столбец, так как при 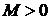 :
: 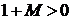 (остальные коэффициенты
(остальные коэффициенты 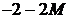 ,
, 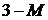 ,
, 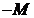 можно считать отрицательными). Разрешающий элемент в
можно считать отрицательными). Разрешающий элемент в  -столбце равен 2:
-столбце равен 2:
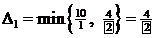 .
.
На первом шаге симплекс-метода происходит смена базиса 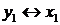 с соответствующими преобразованиями в табл. 7.1. В результате получаем табл. 7.2.
с соответствующими преобразованиями в табл. 7.1. В результате получаем табл. 7.2.
Табл. 7.2
| БП | СЧ |  |  | 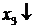 |  |  | 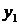 | 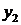 | Преобразования |
 | 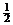 | 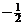 | 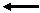 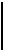 | ||||||
 | 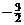 | 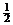 |  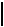 | ||||||
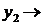 | – 3 | 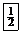 | – 1 | 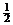 |  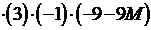 | ||||
 | 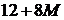 | 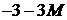 | 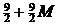 | 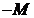 | 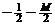 |  |
Базисное решение имеет вид
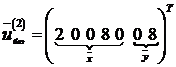 .
.
Проверяем базисное решение 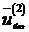 на оптимальность. В качестве разрешающего столбца выберем
на оптимальность. В качестве разрешающего столбца выберем 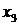 -столбец, так как при
-столбец, так как при 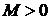 :
: 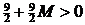 (остальные коэффициенты можно считать отрицательными). Составляем вспомогательное число
(остальные коэффициенты можно считать отрицательными). Составляем вспомогательное число 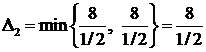 . Заметим, что в качестве разрешающего элемент удобно взять коэффициент в
. Заметим, что в качестве разрешающего элемент удобно взять коэффициент в 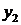 -строке, так как в этом случае искусственная переменная
-строке, так как в этом случае искусственная переменная 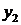 выйдет из базиса. Итак, на втором шаге симплекс-метода происходит смена базиса
выйдет из базиса. Итак, на втором шаге симплекс-метода происходит смена базиса 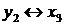 с соответствующими преобразованиями в табл. 7.2. В результате получаем табл. 7.3.
с соответствующими преобразованиями в табл. 7.2. В результате получаем табл. 7.3.
Табл. 7.3
| БП | СЧ |  |  | 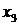 |  | 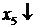 | 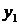 | 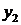 | Преобразования |
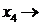 |  |  | – 1 | 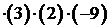 | |||||
 | – 8 | – 3 |    | ||||||
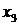 | – 6 | – 2 | |||||||
 | 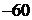 | 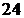 | 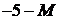 | 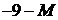 |
Базисное решение имеет вид
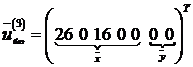 .
.
Проверяем базисное решение 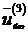 на оптимальность. В качестве разрешающего столбца выберем
на оптимальность. В качестве разрешающего столбца выберем  -столбец. Разрешающий элемент равен 1 и располагается в
-столбец. Разрешающий элемент равен 1 и располагается в  -строке. Происходит смена базиса:
-строке. Происходит смена базиса: 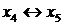 , с соответствующими преобразованиями в табл. 7.3. В результате получаем табл. 7.4.
, с соответствующими преобразованиями в табл. 7.3. В результате получаем табл. 7.4.
Табл. 7.4
| БП | СЧ |  |  | 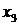 |  |  | 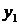 | 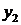 |
 | 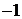 | – 1 | ||||||
 | 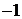 | |||||||
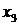 | 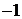 | |||||||
 | 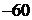 | 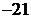 | 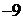 | 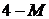 | 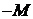 |
Базисное решение имеет вид
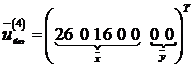 .
.
Построенное базисное решение 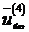 удовлетворяет условию оптимальности, так как в
удовлетворяет условию оптимальности, так как в 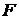 -строке среди коэффициентов при переменных
-строке среди коэффициентов при переменных 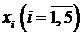 ,
, 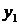 ,
, 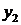 нет ни одного положительного (числа
нет ни одного положительного (числа 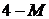 ,
, 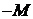 отрицательны в силу выбора
отрицательны в силу выбора 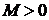 ). Итак, М -задача имеет оптимальное решение
). Итак, М -задача имеет оптимальное решение 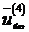 . Согласно теореме 7.1, так как значения искусственных переменных
. Согласно теореме 7.1, так как значения искусственных переменных 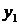 ,
, 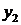 в оптимальном решении равны нулю, то исходная ЗЛП также имеет оптимальное решение
в оптимальном решении равны нулю, то исходная ЗЛП также имеет оптимальное решение 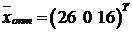 , причем
, причем 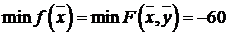 .
.
 2018-01-21
2018-01-21 2613
2613
