Решение типовой задачи

Задача 1. На отрезке ОА длины L числовой оси Ox наудачу поставлены две точки: В (х) и С (у), причем у ≥ х. (Координата точки С для удобства дальнейшего изложения обозначена через у). Найти вероятность того, что длина отрезка ВС меньше длины отрезка ОВ (рис. 2.1.а). Предполагается, что вероятность попадания точки на отрезок пропорциональна длине этого отрезка и не зависит от его расположения на числовой оси.

рис. 2.1

Решение. Координаты точек В и С должны удовлетворять неравенствам 0 ≤ x ≤ L, 0 ≤ y ≤ L, y ≤ x. Введем в рассмотрение прямоугольную систему координат хОу. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей прямоугольному треугольнику ОКМ (рис. 2.1.б). Таким образом, этот треугольник можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек В и С.

Длина отрезка ВС должна быть меньше длины отрезка ОВ, т.е. должно иметь место неравенство у – х < х, или у < 2 х. Последнее неравенство выполняется для координат тех точек фигуры G (прямоугольного треугольника ОКМ), которые лежат ниже прямой у = 2 х (прямая ON). Как видно из рис. 2.1.б, все эти точки принадлежат серому треугольнику ONM. Таким образом, этот треугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию (длина отрезка ВС должна меньше длины отрезка ОВ).

Искомая вероятность

.

Задачи.

2.126. На отрезке L длины 20 см помещен меньший от­резок l длины 10 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Предполагается, что веро­ятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

2.127. На отрезок ОА длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую, чем L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

2.128. В круг радиуса R помещен меньший круг радиуса r. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.

2.129. Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2 а. На плоскость наудачу брошена монета радиуса r < а. Найти вероятность того, что монета не пересечет ни одной из прямых.

2.130. На плоскость с нанесенной сеткой квадратов со стороной а наудачу брошена монета радиуса r < а/2. Найти вероятность того, что монета не пересечет ни одной из сторон квадрата. Предполагается, что вероятность по­падания точки в плоскую фигуру пропорциональна пло­щади фигуры и не зависит от ее расположения.

2.131. На плоскость, разграфленную параллельными пря­мыми, отстоящими друг от друга на расстоянии 6 см, на­удачу брошен круг радиуса 1 см. Найти вероятность того, что круг не пересечет ни одной из прямых. Предпо­лагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

2.132. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что веро­ятность попадания точки в плоскую фигуру пропорцио­нальна площади этой фигуры и не зависит от ее распо­ложения.

2.133. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри впи­санного в круг: а) квадрата; б) правильного треуголь­ника. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга.

2.134. Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти ве­роятность того, что пуля попадет в один из белых сек­торов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фи­гуры.

2.135. На отрезке ОА длины L числовой оси Ох наудачу поставлены две точки В (х) и С (у). Найти вероятность того, что длина отрезка ВС меньше расстояния от точки О до ближайшей к ней точке. Предполагается, что веро­ятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на чис­ловой оси.

2.136. На отрезке ОА длины L числовой оси Ох наудачу поставлены две точки: В(х) и С(у), причем у 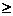х. Найти вероятность того, что длина отрезка ВС окажется меньше, чем L/2. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

2.137. На отрезке ОА длины L числовой оси Ох наудачу поставлены две точки: В (х) и С(у). Найти вероятность того, что длина отрезка ВС окажется меньше, чем L/2. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

2.138. Задача Бюффона (французский естествоиспыта­тель XVIII в.). Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2 a. На плоскость наудачу бросают иглу длины 2l (l < a). Найти вероятность того, что игла пересечет какую-ни­будь прямую.

2.139. На отрезке ОА длины L числовой оси Ох наудачу поставлены две точки: В (х)и С (у). Найти вероятностьтого, что из трех получившихся отрезков можно построить треугольник.

2.140. В сигнализатор поступают сигналы от двух уст­ройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длитель­ностью Т. Моменты поступления сигналов независимы один от другого. Сигнализа­тор срабатывает, если разность между моментами поступления сигналов меньше t (t < Т). Най­ти вероятность того, что сиг­нализатор срабатывает за вре­мя Т, если каждое из уст­ройств пошлет по одному сиг­налу.

2.141. Задача о встрече. Два студента условились встре­титься в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 1/4 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).

2.142. Найти вероятность того, что из трех наудачу взятых отрезков длиной не более L можно построить треугольник. Предполагается, что вероятность попадания точки в пространственную фигуру пропорциональна объему фигуры и не зависит от ее расположения.

Указание. Ввести в рассмотрение пространственную систему координат.

2.145. Наудачу взяты два положительных числа х и у, каждое из которых не превышает двух. Найти вероят­ность того, что произведение ху будет не больше единицы, а частное у/х не больше двух.

2.146. Наудачу взяты два положительных числа х и у, каждое из которых не превышает единицы. Найти веро­ятность того, что сумма х+у не превышает единицы, а произведение ху не меньше 0,09.

2.147. Внутри квадрата с вершинами (0, 0), (1, 0), (1, 1) и (0, 1) наудачу выбирается точка М (х, у). Найти вероятность со­бытия А = {(х, у)| х² + у² а ², а > 0}.

2.148. (продолжение). В условиях предыдущей задачи найти
вероятность события В = {(х, у) | ху < а, а > 0}.

2.149. (продолжение). В условиях задачи 2.147. найти вероятности событий: С = {(х, у) | max (х, у) < а, а > 0}, D =
= {(х, у)| min (х, у) < а, 0 а 1}.

2.150. На перекрестке установлен автоматический светофор,
в котором одну минуту горит зеленый свет и полминуты — красный, затем снова одну минуту — зеленый и полминуты — крас­ный и т. д. В случайный момент времени к перекрестку подъез­жает автомобиль. Какова вероятность того, что он проедет перекресток без остановки?

2.151. Какова вероятность того, что сумма трех наудачу взя­тых отрезков, длина каждого из которых не превосходит l, будет
больше l?

2.152. Луч локатора перемещается в горизонтальной плоско­сти с постоянной угловой скоростью. Какова вероятность того, что цель будет обнаружена в угловом секторе а радиан, если появление цели по любому направлению одинаково возможно?

2.153. Какова вероятность, не целясь, попасть бесконечно ма­лой пулей в прутья квадратной решетки, если толщина прутьев равна а, а расстояние между их осями равно l (l > а)?

2.154. На поверхности шара берут наудачу две точки и соединяют меньшей дугой большого круга. Найти вероятность того, что дуга не превзойдет αрадиан.

2.155. Какова вероятность того, что случайно выбранная на
глобусе точка лежит: а) за полярным кругом (66°33' северной ши­роты); б) между 60° и 30° северной широты; в) между 10° и 40°
западной долготы?

2.156. (задача о встрече).Иван и Петр договорились о встрече в определенном месте между одиннадцатью и двенадцатью часами. Каждый приходит в случайный момент указанного промежутка и ждет появления другого до истечения часа, но не более 15 минут, после чего уходит. Наблюдаемый результат – пара чисел (х, у), где х – время прихода Петра, у – время прихода Ивана (время исчисляется в минутах, начиная от 11 часов). События А = {встреча состоялась}; С = {Ивану не пришлось ждать Петра}. Найти вероятности событий А и С.

2.157. (продолжение задачи о встрече). События D = {встреча состоялась после 11ч. 30мин.}, E = {Иван опоздал на встречу}, F = {встреча состоялась, когда до истечения часа оставалось меньше пяти минут}.Найти вероятности событий D, Е и F.

2.158. Два парохода должны подойти к одному и тому же
причалу. Время прихода обоих пароходов независимо и равно-
возможно в течение данных суток. Определить вероятность того,
что одному из пароходов придется ожидать освобождения причала,
если время стоянки первого парохода — один час, а второго — два
часа.

2.159. В случайный момент времени х [0, Т ]появляется
радиосигнал длительностью t₁. В случайный момент времени
у [0, Т ] включается приемник на время t₂ < t₁. Найти вероятность обнаружения сигнала, если: а) приемник настраивается
мгновенно; б) время настройки приемника равно t₃ (t₃ < t₂ < t₁).

2.160*. Значения а и b равновозможны в квадрате , . Найти вероятности следующих событий: А = {корни квадратного трехчлена х² + 2ах + b действительны}, В = {корни квадратного трехчлена х² + 2ах + b положительны}.

2.161*. Однородный прямой круговой цилиндр с высотой h и радиусом основания r случайным образом бросается на горизон­тальную плоскость. Найти вероятность того, что цилиндр упадет на боковую поверхность.

2.162*. На отрезке длины l наудачу выбираются две точки M₁ и М₂. Определить вероятность того, что из полученных трех отрезков можно построить треугольник.

2.163*. На плоскость с нанесенной на ней квадратной сет­кой многократно бросается монета диаметра d, в результате чего установлено, что в 40 % случаев монета не пересекает ни одной стороны квадрата. Оценить размер сетки.

2.164*. На окружности единичного радиуса наудачу ставятся три точки А, В и С. Какова вероятность того, что треугольник АВС остроугольный?

2.165. Даны две концентрические окружности радиусов
r₂ > r₁. На большей окружности наудачу ставятся две точки А
и В. Какова вероятность того, что отрезок АВ не пересечет малую
окружность?

2.166. Из отрезка [—1, 2] наудачу взяты два числа. Какова
вероятность того, что их сумма больше единицы, а произведение
меньше единицы?

2.167*. (задача Бюффона).На плоскость, разграфленную па­раллельными прямыми линиями, отстоящими друг от друга на расстояние 2а, наудачу бросается игла длиной 2l. Какова веро­ятность того, что игла пересечет одну из параллельных прямых, если l а.

2.168. (парадокс Бертрана).В круге единичного радиуса наудачу проводится хорда. Какова вероятность, что длина хорды окажется больше длины стороны правильного треугольника, впи­санного в данную окружность?