2018-01-21
1018
Случайную величину Х называют дискретной, если множество ее возможных значений конечно или счетно.
Распределение дискретной случайной величины удобно описывать с помощью ряда распределения.
Рядом распределения (вероятностей) дискретной случайной величиныХ называют таблицу (табл. 5.1), состоящую из двух строк: в верхней строке перечислены все возможные значения случайной величины, а в нижней – вероятности 
того, что случайная величина примет эти значения.
| Х | 
| 
| … | 
| … | 
|
| Р | 
| 
| … | 
| … | 
|
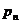
Табл. 5.1
Согласно аксиоме нормированности 
.
Функция распределения F (x) случайной величины Х есть разрывная ступенчатая функция (рис. 5.1), скачки которой соответствуют возможным значениям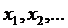 
случайной величины Х и равны вероятностям 
этих значений; между скачками функция F (x) сохраняет постоянное значение. В точке разрыва функция F (x) равна тому значению, с которым она подходит к точке разрыва слева (рис. 5.1) эти значения помечены точками). Функция F (x) «непрерывна слева», т.е. при подходе к любой точке слева не терпит разрыва, а при подходе справа может терпеть разрыв.
рис. 5.1
Вероятность попадания случайной величины Х на участок от 
до 
(включая ) выражается через функцию распределения формулой
,
или в других обозначениях,
,
где знаком [ обозначено то, что точка включается в состав отрезка от до , а знаком) – что точка в него не включается.
Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех ее возможных значений 
на соответствующие вероятности 
:
.
Математическое ожидание случайной величины может и не существовать, если соответствующая сумма расходится. В случае, когда надо математическое ожидание случайной величины Х обозначить одной буквой, будем писать
.
Центрированной случайной величиной называется разность между случайной величиной Х и ее математическим ожиданием:
.
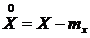Дисперсией случайной величины Х называется математическое ожидание квадрата соответствующей центрированной случайной величины:
.
Для дискретной случайной величины Х дисперсия вычисляется по формуле
.
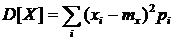В случае, когда надо дисперсию случайной величины Х обозначить одной буквой, мы будем обозначать ее 
.
Средним квадратическим отклонением (или стандартом) случайной величины Х называется корень квадратный из ее дисперсии:
(подразумевается арифметическое или положительное значение корня).
Начальным моментом k -го порядка случайной величины Х называется математическое ожидание k -ой степени этой случайной величины:
.
Для дискретной случайной величины Х начальный момент может вычисляться по формуле
.
Центральным моментом k -го порядка случайной величины называется математическое ожидание k -ой степени соответствующей центрированной величины:
.
Для дискретной случайной величины Х центральный момент может вычисляться по формуле
.
Математическое ожидание случайной величины Х есть ее первый начальный момент, а дисперсия – второй центральный:
.
Центральные моменты выражаются через начальные моменты
Особенно важна первая из трех формул, выражающая дисперсию через второй начальный момент
или в другом написании
,
т.е. дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания.
Индикатором события А называется дискретная случайная величина U, имеющая два возможных значения: 0 и 1, равная 0 если событие А не появилось, и единице, если появилось:
.
Ряд распределения индикатора U события А имеет вид
| q | p |
U:
где p – вероятность события в данном опыте; q = 1 – p.
Математическое ожидание и дисперсия величины U равны соответственно
.
В ряде задач теории вероятностей пользование индикаторами событий существенно упрощает решение.
При вычислении числовых характеристик случайных величин часто бывает удобно пользоваться формулой полного математического ожидания: если об условиях опыта можно сделать п несовместных гипотез 
, полное математическое ожидание случайной величины Х может быть вычислено по формуле
(*)
где 
- условное математическое ожидание величины Х при гипотезе 
.
Формулу полного математического ожидания можно применять при вычислении начальных моментов любого порядка:
.
Пользоваться этой формулой в принципе можно и при вычислении центральных моментов любого порядка:
,
но не забывать при этом, что величина 
в последней формуле должна вычисляться как 
, где 
- безусловное математическое ожидание случайной величины Х, выражаемое формулой (*), а не условное при гипотезе 
.
Примеры законов распределения дискретных случайных величин:
1. Биномиальное распределение. Случайная величина Х называется распределенной по биномиальному закону, если ее возможные значения 0,1,…, m,… n, а соответствующие вероятности
, (5.1.1)
где 0 < p < 1, q =1 – p; m = 0, 1, …, n. Распределение (5.1.1) зависит от двух параметров: p и n.
Для случайной величины Х, имеющей биномиальное распределение с параметрами p и n
, (5.1.2)
где q =1 – p.
2. Распределение Пуассона. Дискретная случайная величина Х называется распределенной по закону Пуассона, если ее возможные значения 0,1,…, m,…, а вероятность события { X = m } выражается формулой
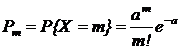(m = 0, 1, 2, …), (5.1.3)
где a > 0. Распределение Пуассона зависит от одного параметра а. Для случайной величины Х, распределенной по закону Пуассона,
. (5.1.4)
Пуассоновское распределение является предельным для биномиального при 
, если 
. Этим распределением можно пользоваться приближенно, если производится большое число независимых опытов, в каждом из которых событие А происходит с малой вероятностью.
Пуассоновскому закону распределения подчиняется также количество точек, попадающих в заданную область пространства (одномерного, двумерного или трехмерного), если случайное расположение точек в этом пространстве удовлетворяет некоторым ограничениям.
Одномерный вариант встречается при рассмотрении «потоков событий». Потоком событий называют последовательность однородных событий, наступающих одно за другим в случайные моменты времени.
Среднее число событий 
, приходящихся на единицу времени, называется интенсивностью потока. Величина может быть как постоянной, так и переменной 
.
Поток событий называется потоком без последействия, если вероятность попадания того или иного числа событий на какой-то участок времени не зависит от того, сколько событий попало на любой другой непересекающийся с ним участок.
Поток событий называют ординарным, если вероятность появления на элементарном участке 
двух или более событий пренебрежимо мала по сравнению с вероятностью появления одного события.
Ординарный поток событий без последействия называется пуассоновским. Если события образуют пуассоновский поток, то число Х событий, попадающих на любой участок времени 
, распределено по закону Пуассона:
(5.1.5)
где а – математическое ожидание числа точек, попадающих на участок;
- интенсивность потока.
Если 
, пуассоновский поток называется стационарным пуассоновским или простейшим. Для простейшего потока число событий, попадающих на любой участок времени длины 
распределено по закону Пуассона с параметром 
.
Случайным полем точе к называется совокупность точек, случайным образом разбросанных на плоскости (или в пространстве).
Поле точек называется пуассоновским, если оно обладает свойствами:
1) вероятность попадания того или иного числа точек в любую область плоскости (пространства) не зависит от того сколько их попало в любую область, не пересекающуюся с данной;
2) вероятность попадания в элементарную область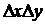 
двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (свойство ординарности).
Число Х точек пуассоновского поля, попавших в любую область S плоскости (пространства) распределено по закону Пуассона:
, (5.1.6)
где а – математическое ожидание числа точек, попадающих в область S. Если интенсивность поля 
, поле называется однородным (свойство аналогичное стационарности потока событий). При однородном поле с интенсивностью 
имеем 
, где s – площадь (объем) области S. Если поле неоднородно, то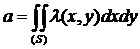 
(для плоскости); 
(для пространства).
Для вычислений, связанных с распределением Пуассона, удобно пользоваться таблицами функции и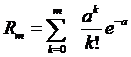 
. Последняя функция выражает вероятность того, что случайная величина Х, имеющая распределение Пуассона с параметром а, примет значение, не превосходящее m: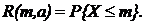 
3. Геометрическое распределение. Говорят, что случайная величина Х имеет геометрическое распределение, если ее возможные значения 0,1,…, m,…, а вероятности этих значений
, (5.1.7)
где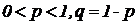 
.
Вероятности 
для ряда последовательных значений m образуют бесконечно убывающую геометрическую прогрессию со знаменателем q. На практике геометрическое распределение встречается, когда производится ряд независимых «попыток» достигнуть какого-то результата А; при каждой «попытке» результат достигается с вероятностью p. Случайная величина Х – число «бесполезных» попыток (до первого опыта, в котором появится событие А).
Ряд распределения случайной величины Х имеет вид
Математическое ожидание случайной величины Х, имеющей геометрическое распределение, равно
(5.1.8)
а ее дисперсия
(5.1.9)
Нередко рассматривают случайную величину Y = X + 1, равную числу попыток до получения результата А, включая удавшуюся. Распределение случайной величины Y имеет вид
(5.1.10)
(5.1.11)
Распределение случайной величины Y = X + 1 будем называть в дальнейшем «геометрическим распределением, начинающемся с единицы».
4. Гипергеометрическое распределение. Случайная величина Х с возможными значениями 0,1,…, m,…, а имеет гипергеометрическое распределение с параметрами n, a, b, если
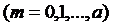(5.1.12)
При использовании этой формулы надо полагать, 
, если r > k.
Гипергеометрическое распределение возникает при следующих условиях: имеется урна, в которой а белых и b черных шаров; из нее вынимается n шаров. Случайная величина Х – число белых шаров среди вынутых; ее распределение выражается формулой (5.1.12).
Математическое ожидание случайной величины, имеющей распределение (5.1.12), равно
(5.1.13)
а ее дисперсия
(5.1.14)
