Решение типовых задач

Задача 1. Дан график функции распределения случайной величины Х (рис. 5.14). Построить на том же графике функцию распределения случайной величины Y = -X.

Решение.

Для построения графика функции нужно кривую зеркально отразить в оси ординат и каждую ординату вычесть из единицы.

 

рис. 5.14

Задача 2. В пространстве трех измерений случайным образом расположены точки. Число точек в некотором объеме пространства есть случайная величина, подчиненная закону Пуассона с математическим ожиданием , где - среднее число точек, находящихся в единичном объеме. Требуется найти закон распределения расстояния R от любой точки пространства до ближайшей к ней случайной точки.

Решение. Функция распределения F(r) есть вероятность того, что в сферу радиуса r попадет хотя бы одна точка:

где - объем сферы радиуса r; отсюда

Задача 3. Имеется случайная величина Х, подчиненная нормальному закону с математическим ожиданием m и средним квадратическим отклонением . Требуется приближенно заменить нормальный закон равномерным в интервале ; границы 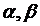подобрать так, чтобы сохранить неизменными случайные характеристики величины Х: математическое ожидание и дисперсию.

Решение. Для равномерного распределения на участке

Решая эти уравнения относительно , имеем

; .

Задача 4. В теории надежности технических устройств в качестве закона распределения времени безотказной работы устройства часто применяется закон Вейбулла с функцией распределения

, (5.6.9)

где - некоторая константа; n – целое положительное число. Найти 1) плотность f(x); 2) математическое ожидание и дисперсию случайной величины Х, распределенной по закону Вейбулла:

Решение.

1) 2) .

Делаем замену переменной

,

где - неизвестная гамма-функция.

;

.

 

Задачи.

5.105. Может ли при каком-либо значении аргумента быть: 1) функция распределения больше единицы? 2) плотность распределения больше единицы? 3) функция распределения отрицательной? 4) плотность распределения отрицательной?

5.106. Какова размерность: 1) функции распределения; 2) плот­ности распределения; 3) математического ожидания; 4) дисперсии; 5) среднего квадратического отклонения; 6) третьего начального момента?

5.107. Дан график плотности f_x (x)случайной величины X (рис. 5.15). Построить на том же графике плотность f_у (x)случайной величины Y = X + а, где а — неслучайная величина. Написать выражение для f_у (x).

рис. 5.15

5.108. Построить функцию распределения F (х) для случайной вели­чины, распределенной равномерно на участке (а, b).

5.109. Случайная величина X распределена по «закону прямоуголь­ного треугольника» в интервале (0, а) (рис. 5.16). 1) Написать выраже­ние плотности f (х); 2) найти функцию распределения F (х); 3) найти вероятность попадания случайной величины X на участок от а/2 до а; 4) найти характеристики величины X: т_х, D_x, σ_x, μ₃ [ X ].

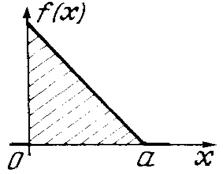
рис. 5.16

5.110. Случайная величина X подчинена закону Симпсона («закону равнобедренного треугольника») на участке от — а до а (рис. 5.17). 1) Написать выражение плотности распределения; 2) построить гра­фик функции распределения; 3) найти числовые характеристики слу­чайной величины X: т_х, D_x,, σ_x, μ₃ [ X ]; 4) найти вероятность попа­дания случайной величины X в интервал (— а /2, а).

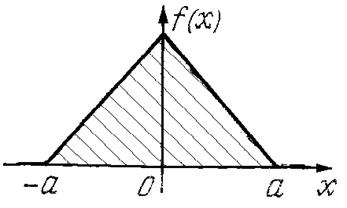
рис. 5.17

5.111. Случайная величина X распределена по закону Коши: f (х) = а/ (1 + х²).1) Найти коэффициента; 2) найти функцию распре­деления F (х);3) найти вероятность попадания величины Х на учас­ток (—1, +1); 4) существуют ли для случайной величины X числовые характеристики: математическое ожидание и дисперсия?

5.112. Случайная величина X подчинена показательному закону распределения с параметром μ: f (x) = μе^-μx при х > 0. 1) Построить кривую распределения; 2) найти функцию распределения F (х)и по­строить ее график; 3) найти вероятность того, что случайная величина X примет значение меньшее, чем ее математическое ожидание.

5.113. Случайная величина Х подчинена закону Лапласа f (x) = ае^-λ|х| где λ – положительный параметр. 1) Найти коэффициент а; 2) построить графики плотности и функции распределения; 3) найти т_х, D_x.

5.114. Случайная величина R – расстояние от точки попадания до центра мишени – распределена по закону Рэлея: при r > 0 (рис 5.18).

рис.5.18

Найти 1) коэффициент А; 2) моду M случайной величины R; 3) т_r и D_r 4) вероятность того, что в результате выстрела расстояние от точки попадания до центра мишени окажется меньше, чем мода.

5.115. Случайная величина X с вероятностью р₁ имеет плотность f₁ (х),а с вероятностью р₂ — плотность f₂ (х) (р₁ + р₂ = 1). Написать выражение для плотности и функции распределения величины X. Най­ти ее математическое ожидание и дисперсию.

5.116. Браковка шариков для подшипников производится следую­щим образом: если шарик не проходит через отверстие диаметром d₁, но проходит через отверстие диаметром d₂ > d_], то его размер счита­ется приемлемым. Если какое-нибудь из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика D есть нормально распределенная случайная величина с характеристиками m_d = (d₁ + d₂)/2и σ _d = (d₂ — d₁)/4. Определить вероятность р того, что шарик будет забракован.

5.117. В условиях предыдущей задачи найти среднее квадратическое отклонение σ_d диаметра шарика, если известно, что брак состав­ляет 10% всей продукции.

5.118. При работе ЭВМ в случайные моменты возникают неисправ­ности. Время Т работы ЭВМ до первой неисправности распределено по показательному закону с параметром : (t > 0). При возникновении неисправности она мгновенно обнаруживается и ЭВМ поступает в ремонт. Ремонт продолжается время t₀, после чего ЭВМ снова включается в работу. Найти плотность f (t)и функцию распре­деления F (t) промежутка времени Z между двумя соседними неисп­равностями. Найти его математическое ожидание и дисперсию. Найти вероятность того, что Z будет больше 2 t₀.

5.119. Время Т между двумя сбоями ЭВМ распределено по показа­тельному закону с параметром λ: f (t)= λе^-λt при (t > 0). Решение определенной задачи требует безотказной работы машины в течение времени τ. Если за время τ произошел сбой, то задачу приходится ре­шать заново. Сбой обнаруживается только через время τ после начала решения задачи. Рассматривается случайная величина - время, за которое задача будет решена. Найти ее закон распределения и математическое ожидание (среднее время решения задачи).

5.120. В условиях предыдущей задачи найти вероятность того, что за данное время t = k τ будет решено не менее m задач (m < k).

5.121. Доказать, что закон распределения расстояния между сосед­ними событиями в простейшем потоке с интенсивностью λ — показа­тельный, с параметром λ.

5.122. Рассматривается пуассоновское поле точек на плоскости с постоянной плотностью λ. Найти закон распределения и числовые характеристики m_r, D_r расстояния R от любой точки поля до ближай­шей к ней соседней точки.

5.123. В некотором звездном скоплении звезды образуют трехмер­ное пуассоновское поле точек с плотностью λ (среднее количество звезд в единице объема). Фиксируется одна (произвольная) звезда и рассмат­риваются: ближайшая от нее звезда, следующая (вторая) по удален­ности, третья и т. д. Найти закон распределения расстояния R_n от данной звезды до n -й в этом ряду.

5.124. Деревья в лесу растут в случайных точках, которые образу­ют пуассоновское поле с плотностью λ (среднее число деревьев на еди­ницу площади). Выбирается произвольная точка О в этом лесу. Рас­сматриваются случайные величины:

R₁ — расстояние от точки О до ближайшего к ней дерева;

R₂ — расстояние от точки О до следующего по порядку (второго по удаленности) дерева;

…………………………………………………………………………………

R_n — расстояние от точки О до п- гопо удаленности дерева. Найти закон распределения каждой из этих случайных величин.

5.125. На перекрестке стоит автоматический светофор, в котором 1 мин горит зеленый свет и 0,5 мин — красный, затем опять 1 мин го­рит зеленый свет, 0,5 мин — красный и т. д. Некто подъезжает к пе­рекрестку на машине в случайный момент, не связанный с работой светофора. 1) Найти вероятность того, что он проедет перекресток, не останавливаясь; 2) найти закон распределения и числовые характе­ристики времени ожидания у перекрестка Т_ож; 3) построить функцию распределения F (t)времени ожидания Т_ож.

5.126. Нормальная функция распределения. Случайная величина X имеет нормальное распределение с параметрами m, σ. Найти ее функ­цию распределения F (х).

5.127*. Показать, что функция вида при x > 0. [α > 0 и а > 0 – некоторые постоянные и s – натуральное число (s = 1, 2, 3, …)] обладает свойствами плотности распределения. Определить параметры а и α исходя из заданного математического ожидания m_x и найти D_x.

5.128*. Моменты нормального закона. Имеется случайная вели­чина X, распределенная по нормальному закону с параметрами т и σ. Найти выражение для величины α_s [X] — начального момента s-гo порядка.

5.129. Случайная величина X имеет нормальное распределение с параметрами т и σ. Написать выражение для ее функции распределе­ния F (х) = Р { X < х }. Написать выражение для функции распреде­ления Ψ (у)= Р (Y < y) случайной величины Y = - X.

5.130*. Функция распределения F (x)неотрицательной случайной величины X задана графиком (рис. 5.18). Математическое ожидание случайной величины X равно m_x. Показать, что m_x геометрически мо­жет быть представлено площадью фигуры, заштрихованной на рис. 5.19 (ограниченной кривой у = F (х), прямой у = 1 и осью орди­нат).

рис. 5.19

5.131. Случайная величина X подчинена нормальному закону с ма­тематическим ожиданием т = 0 (рис. 5.20). Задан интервал , не включающий начала координат. При каком значении среднего квадратичного отклонения σ вероятность попадания случайной величины X в интервал достигает максимума?

рис. 5.20

5.132. Имеется случайная величина X, подчиненная нормальному
закону с математическим ожиданием т и средним квадратичным отклонением σ. Требуется приближенно заменить нормальный закон равномерным в интервале ; границы подобрать так, чтобы сохранить неизменными основные характеристики случайной величины X:
математическое ожидание и дисперсию.

5.133. Непрерывная случайная величина X имеет плотность f (х) .
В результате опыта обнаружено, что появилось событие 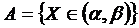)} [случайная величина X попала на участок ]. Найти условную плотность f_A (х)случайной величины X при наличии события А.

5.134. На производстве изготавливаются однородные детали, номи­нальный размер которых l₀, но фактически наблюдаются от этогораз­мера случайные отклонения, распределенные по нормальному закону с математическим ожиданием m = 0 и средним квадратическим откло­нением σ. При контроле бракуются все изделия, размеры которых от­личаются от номинального больше, чем на допуск Δ. Найти вероятность события А = {изделие будет забраковано}. Найти и построить плот­ность вероятности для размера изделия, прошедшего контроль.

5.135. Надежность р радиотехнического устройства зависит как от общего времени τ, прошедшего с момента включения устройства, так и от того, вышел ли из строя в какой-то момент t < τ стабилизатор на­пряжения. Если стабилизатор напряжения не вышел из строя до мо­мента τ, надежность задается функцией р = р₀ (τ); если же он вышел из строя в момент t < τ, то надежность есть функция двух аргументов; р = р₁ (τ, t).Время безотказной работы стабилизатора есть случайная величина Т с плотностью f (t). Найти функцию распределения F _Θ(x)времени Θ безотказной работы устройства и его математическое ожи­дание m _Θ.

5.136. Ожидается поступление по радиоканалу какого-то сообщения S; момент Т поступления этого сообщения случаен и имеет плотность f (t). В какой-то момент τ обнаружено, что сообщение еще не поступи­ло. Найти при этом условии плотность распределения φ (t)времени Θ, которое остается до поступления сообщения S.

5.137. Момент Т наступления какого-то события А есть случайная величина, распределенная по показательному закону: (t > 0). В момент τ стало известно, что событие А еще не произошло. Найти условную плотность φ (t) времени Θ, которое осталось до наступления события.

5.138. Вероятность отказа радиолампы в момент включения зависит от напряжения U в схеме и равна q (U), Напряжение U случайно и имеет нормальное распределение с параметрами и₀ и σ_u. Найти полную вероятность q отказа радиолампы в момент включения.

5.139. Случайное напряжение U, имеющее плотность f (u), пропускается через ограничитель, который «срезает» все значения напряжения, меньшие чем u₁ и большие чем и₂, в первом случае повышая его до u₁, а во втором — понижая до и₂. Найти распределение случайной величины Ũ — напряжения, прошедшего через ограничитель, и найти его математическое ожидание и дисперсию.

5.140. По радиоканалу передается сообщение длительностью l (рис. 5.21). Для того чтобы «забить» это сообщение, осуществляет­ся помеха длительностью b > l, рассчитанная так, чтобы центр помехи О₁ совпал с центром сообщения О.

Фактически из-за случайных ошибок центр помехи смещен относи­тельно центра сообщения на X. Случайная величина X распределена нормально с параметрами m = 0, σ = l/ 2. Найти распределение слу­чайной величины U — длины части сообщения, «забитого» помехой, найти математическое ожидание т_u,дисперсию D_u и среднее квадратическое отклонение σ_и.

рис. 5.21

5.141. Случайная величина X с вероятностью р₁ имеет плотность f₁ (х),с вероятностью р₂ — плотность f₂ (x),..., с вероятностью р_i — плотность f_i (x) (i = 1,..., n). Найти полную (среднюю) плотность случайной величины X.

5.142. Случайная величина X с вероятностью 0,4 имеет нормаль­ное распределение с параметрами т = 0 и σ = 2, а с вероятностью 0,6 — нормальное распределение с параметрами т =2 и σ = 1. Най­ти плотность распределения случайной величины X.

5.143. Имеются две случайные величины: дискретная X с рядом распределения

и непрерывная Y с плотностью f (у).Величины X и Y принимают свои значения независимо друг от друга. Является ли их сумма Z = X + Y дискретной, непрерывной или смешанной случайной вели­чиной? Найти ее распределение.

5.144. Дискретной, непрерывной или смешанной является величина Z = min { X, а },где X — непрерывная случайная величина с плотно­стью f (x); а — неслучайная величина? Найти распределение случай­ной величины Z, ее математическое ожидание и дисперсию.

5.145. Из двух источников А и В посылаются периодические сигна­лы одинаковой длительности l и с одинаковыми интервалами L между ними (рис. 5.22); l < L. Моменты передачи сообщений из источников А и В несогласованны. Сообщения, передаваемые источниками, при наложении искажаются. Найти 1) вероятность R того, что хотя бы одно сообщение будет искажено (полностью или частично); 2) вероят­ность того, что будет искажено не более 10 % каждого сообщения; 3) функцию распределения случайной величины Z — «доля искаженно­го текста»; 4) среднюю долю искаженного текста .

рис. 5.22

5.146. Имеется непрерывная случайная величина X с плотностью f (x) (рис. 5.23). Наблюденное значение случайной величины сохра­няется, если оно попало в интервал (х₁, х₂), и отбрасывается, если оно вышло за пределы интервала (х₁, х₂). Получается новая случайная величина X («урезанная» случайная величина X) с диапазоном зна­чений от х₁ до х₂. Найти плотность случайной величины .

рис. 5.23

5.147. Одна женщина утверждает: «Мой муж среднего роста, а ведь большинство мужчин ниже среднего роста». Бессмысленно ли это утверж­дение?

5.148. Срок службы технического устройства есть случайная величина Т с плотностью f (t) (t > 0). В момент t₀, если устройство до этого момента еще не отказало, проводится его профилактический ремонт, после чего оно работает еще время Т₁ с плотностью f₁ (t). Если устройство отказало в какой-то момент u < t₀, то немедленно производится аварийный ремонт, после которого устройство работает еще случайное время Т₂ с плотностью f₂ (t) (второго ремонта уже не производится). Найти математическое ожидание времени θ, которое проработает устройство (в него не включается время, затрачиваемое на ремонт).

5.149. По радиоканалу передается последовательность сообщений одинаковой длины l (рис. 5.24, а) со случайными промежутками Т₁, Т₂, … между ними. Интервалы Т₁, Т₂, … имеют одинаковое распределение. Время от времени в сообщения вмешиваются случайные помехи (рис. 5.24, б). Моменты возникновения и прекращения помех никак не связаны с последовательностью сообщений. Длительность D каждой помехи случайна и распределена по показательному закону с параметром μ; длительность интервала между помехами тоже случайна и распределена по показательному закону с параметром v. Если помеха захватывает все сообщение или его часть искажается либо все сообщение, либо соответствующая его часть. Найти среднюю долю сообщения, которая будет искажена помехами, т.е. отношение средней длины искаженного текста к средней длине переданного.

рис. 5.24

5.150. За время τ (продолжительность наблюдения) сигнал при­ходит с вероятностью р; сигнал появляется в любой точке промежутка τ с одинаковой плотностью вероятности. Известно, что в момент t < τ (рис. 5.25) сигнал еще не появился. Найти вероятность Q того, что он появится за оставшееся время τ — t.

рис. 5.25

5.151. Момент прихода сигнала — случайная величина Т с плот­ностью f (t).В какой-то момент t < τ сигнал еще не пришел. Найти вероятность того, что он придет за последующий участок времени t до τ (рис. 5.26).

рис. 5.26

5.152. В условиях предыдущей задачи f (t) – нормальное распределение с параметрами m, σ; t = m (т.е. сигнал не пришел за время m). Найти вероятность того, что он придет за промежуток времени длиной σ, непосредственно следующий за t = m. Задача имеет смысл, только когда Т – величина практически неотрицательная, т.е. при m - 3 σ > 0.

5.153. Случайная величина подчинена закону равномерного распределения на интервале [0; 2]. Написать выражение для плотности вероятности и функции распределения случайной вели­чины X. Найти вероятность неравенства 0 < Х < 1/2. Как изменяется плотность вероятности на интервале [0; 2] при условии, что случайная величина на этом интервале имеет равномерное распределение? Из какого соотношения можно определить по плотности вероятности функцию распределения случайной величины?

5.154. Точку бросают наудачу внутрь круга радиуса R. Вероят­ность ее попадания в любую область, расположенную внутри круга, пропорциональна площади этой области. Найти функцию распределения расстояния точки до центра круга. Чему равна вероятность того, что случайная величина X — расстояние от случайной точки внутри круга до центра — принимает значение меньше ? Чему равна вероятность Р (Х < х),где x — радиус круга, центр которого совпадает с центром круга радиуса R ()?

5.155. Плотность вероятности f (x)случайной величины X опре­деляется формулой (распределение Лапласа) . Определить: а) коэффициент а; б) математическое ожидание т_х и
дисперсию D_x. Чему равен интеграл от плотности вероятности по всей области возмож­ных значений случайной величины X? Каким свойством обладает интеграл по симметричному интервалу относительно начала координат, если подынтегральная функция является: а) чет­ной; б) нечетной?

5.156. Случайная величина X имеет равномерное распределение с математическим ожиданием т_х = 1и дисперсией D_x = 3. Найти плотность вероятности случайной величины X. Чему равно математическое ожидание случайной величины X, равномер­но распределенной на интервале [ а, b ]? Чему равна дисперсия случайной величины X?

5.157. Плотность вероятности случайной величины Х задана следующим образом:

Найти постоянную величину а и вероятность того, что в двух независимых испытаниях случайная величина примет значения больше . Чему равен интеграл от плотности вероятности по области возможных
значений случайной величины X? Чему равна вероятность того, что при одном испытании случайная вели­чина X примет значение больше ?

5.158. На окружности радиуса R с центром в начале координат берется наудачу точка. Вероятность того, что точка взята на ка­кой-либо дуге окружности, зависит только от длины этой дуги и пропорциональна ей. Взятая точка проектируется на ось абсцисс. Найти функцию распределения и плотность вероятности случайной величины X. Какому положению точки на окружности (рис. 5.27) соответствует нера­венство Х < х? Чему равна длина дуги ABC? Чему равно отношение длины дуги ABC к длине окружности?

 

 

 

рис. 5.27

5.159. Функция распределения непрерывной случайной величины задана выражением

Найти коэффициент а и плотность вероятности случайной величины Х. Определить вероятность неравенства 0 < X < 1.

5.160. Плотность вероятности случайной величины X задана
выражением

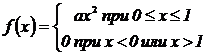
Найти коэффициент а. Определить вероятность неравенства 0 < X <1/4.

5.161. Функция распределения случайной величины X имеет
вид (закон арксинуса)

Определить постоянные а и b. Найти плотность вероятности случайной величины X и построить ее график.

5.162. Плотность вероятности случайной величины X задана
выражением

Найти коэффициент а. Определить математическое ожидание т_х и дисперсию D_x.

5.163. Функция распределения случайного времени безотказной работы радиоаппаратуры имеет вид (показательное распреде­ление) . Найти вероятность безотказной работы аппаратуры в течение времени Т.

5.164. Случайная величина X имеет плотность вероятности (закон Коши)

Требуется: а) найти коэффициент а и функцию распределения F (x); б) найти вероятность неравенства ; в) определить математическое ожидание, моду и медиану этого распределения.

5.165. Плотность вероятности случайной величины X задана выражением

Найти коэффициент а. Определить вероятность того, что в ре­зультате опыта случайная величина X отклонится от своего мате­матического ожидания не более чем на 0,5.

5.166. Случайная величина X распределена по закону Рэлея с плотностью вероятности

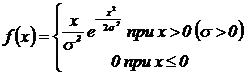
Найти: а) функцию распределения случайной величины X; б) моду и медиану этого распределения.

5.167. Точку бросают наудачу внутрь шара радиуса R. Вероятность ее попадания в любую область, расположенную внутри
шара, пропорциональна объему этой области. Найти функцию
распределения, плотность вероятности, математическое ожидание
и дисперсию расстояния точки до центра шара.

5.168. Модуль вектора скорости молекулы газа есть случайная
величина, распределенная по закону Максвелла с плотностью вероятности

Найти среднюю скорость и дисперсию величины скорости мо­лекулы.

5.169. График плотности вероят­ности случайной величины X изображен на рис. 5.28 (закон Симпсона). Написать выражение плот­ности вероятности и функцию распределения этой случайной величины; найти ее математическое ожидание и дисперсию.

рис. 5.28

5.170. Случайная величина X имеет равномерное распределение
с математическим ожиданием m_x = 3 и дисперсией D_x = 4/3.
Найти функцию распределения случайной величины X.

5.171. На поверхности сферы берут наудачу две точки и сое­диняют их меньшей дугой большого круга. Найти функцию распределения, плотность вероятности, математическое ожидание и дисперсию длины дуги.

5.172. Случайная величина X удовлетворяет неравенству - 2 2. Известно, что каждое из значений —2 и 2 она
принимает с вероятностью 1/8. Кроме того, в интервале (- 2; 2)
случайная величина X имеет равномерное распределение. Соста­вить функцию распределения случайной величины X и построить
ее график.

5.173*. Случайная величина X непрерывного типа неотри­цательна, имеет конечное математическое ожидание и ее закон распределения задан функцией распределения F_Х (x).Показать, что математическое ожидание такой случайной величины может быть записано в виде

.

5.174. Плотность распределения вероятностей f_Х (x)не­которой С.В.Н.Т. X удовлетворяет следующим условиям: f_Х (x) = 0 при | х | , на отрезке функция f_Х (x)— четная кусочно-непрерывная функция. Показать, что для ее дисперсии справедлива формула

.

где α_k — коэффициенты Фурье разложения функции f_Х (x)по системе {cos kx, k = 0, 1, …}.

5.175. Пусть X — С.В.Н.Т. с унимодальным законом рас­пределения. Обозначим = М [(X — d_X)²](центральный момент второго порядка относительно моды), 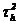= М [(X — h_X)²](центральный момент второго порядка относительно медианы). Пусть, кроме того, d_X ≠ h_X. Показать, что для равенства этих моментов необходимо и достаточно, чтобы

5.176. Для равномерно распределенной на [ a, b ]случай­ной величины X вычислить функцию распределения, мате­матическое ожидание, медиану, дисперсию, коэффициент эксцесса.

5.177. Шкала рычажных весов, установленных в лабора­тории, имеет цену делений 1 г. При измерении массы хими­ческих компонентов смеси отсчет делается с точностью до целого деления с округлением в ближайшую сторону. Ка­кова вероятность, что абсолютная ошибка определения массы: а) не превысит величины среднеквадратичного от­клонения возможных ошибок определения массы; б) будет заключена между значениями σ _Х и 2σ _Х?

5.178*. Пусть X — время безотказной работы радио­электронной аппаратуры. Примем, что вероятность выхода из строя аппаратуры в течение времени Δ х с точностью до величины о (Δ х) равна λ, Δ х (λ> 0) независимо от времени х, в течение которого аппаратура уже проработала до рассматриваемого интервала времени Δ х. Вычислить функцию распределения случайной величины X.

5.179. Время безотказной работы радиоаппаратуры является случайной величиной X, распределенной по показательному закону с параметром λ, Вычислить математическое ожидание, дисперсию и вероятность того, что радио­аппаратура не выйдет из строя в течение времени t = т_Х.
Квантилью какого порядка для данного распределения является значение т_Х?

5.180. Случайная величина X распределена по показательному закону с параметром X. Вывести рекуррентную формулу, выражающую центральный момент (k + 1)-го порядка через центральный момент k- гопорядка и математическое ожидание, и с ее помощью вычислить коэффициент асимметрии и коэффициент эксцесса показательного рас­пределения.

5.181. Время ожидания у бензоколонки автозаправочной
станции является случайной величиной X, распределенной
по показательному закону со средним временем ожидания,
равным t₀. Найти вероятности следующих событий:

5.182. В некоторых капиталистических странах действу­ет закон о налогообложении, который распространяется на тех частных предпринимателей, годовой доход которых превосходит некоторый установленный законом уровень х₀. Считая, что годовой доход наудачу выбранного лица, облагаемого налогом, является случайной величиной X, распре­деленной по закону Парето с параметрами а = 4, х₀ = 1000, найти вероятности следующих событий: А = { h_x X < т_х }, В = {| X — т_X | < σ _X }.Критиче­ской точкой какого порядка для данного распределения
является математическое ожидание т _X?

5.183. Случайная величина X распределена по закону Коши, определяемому функцией распределения вероятностей

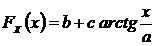при .

Выбрать коэффициенты а, b и с таким образом, чтобы данное распределение соответствовало случайной величине непре­рывного типа, и вычислить плотность вероятности такого распределения. Существуют ли математическое ожидание и моменты более высокого порядка у данного распределе­ния? Найти моду, медиану и квантиль t_p порядка р = 0,75.

5.184. Случайная величина X распределена по закону .Пользуясь таблицей функции Лапласа, вычислить вероятность p_k того, что отклонение величины X от ее математического ожидания не превзойдет величины kσ
(ответ получить для трех значений k = 1, 2, 3).

5.185. Измеряемая случайная величина X подчиняется
закону распределения N (10, 5). Найти симметричный отно­сительно т_X интервал, в который с вероятностью р попадет измеренное значение. Рассмотреть следующие числовые значения: а) р = 0,9974; б) р = 0,9544; в) р = 0,50.

5.186. В нормально распределенной совокупности 15 % значений х меньше 12 и 40 % значений х больше 16,2. Найти среднее значение и стандартное отклонение данного распре­деления.

5.187. Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от номинала не превышает 10 мм. Случайные отклонения контроли­руемого размера от номинала подчиняются закону N (0, 5).

а) Сколько процентов годных деталей изготовляет ав­томат?

б) Сколько необходимо изготовить деталей, чтобы с ве­роятностью не менее 0,95 среди них оказалась хотя бы одна бракованная деталь?

5.188. Браковка шариков для подшипников произво­дится следующим образом: если шарик проходит через отверстие диаметра d₂, но не проходит через отверстие диа­метра d₁ < d₂, то шарик считается годным. Если какое-либо из этих условий нарушается, то шарик бракуется. Считается,
что диаметр шарика X — случайная величина, распределенная по закону , где параметр (0 < < 1/2) определяет точность изготовления шариков.

а) Определить вероятность того, что шарик будет забра­кован.

б) Какую точность изготовления следует установить (т. е. каким следует выбрать параметр , чтобы брак со­ставлял не более 2 % всей продукции?

5.189. Случайная величина X распределена по закону N (m, σ).

а) Вычислить 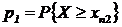и . где х_п1 и х_{п 2} — точки перегиба кривой плотности распределения вероятностей.

б)** Пусть (а, b)— интервал, не содержащий т_X. При каком σ вероятность 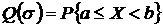будет наи­большей?

в)* Доказать рекуррентное соотношение () для центральных моментов.

г) Вычислить первый абсолютный центральный момент (М (| Х - m_X |)).

5.190*. Случайная величина X распределена по закону N (—1, 1). Вычислить коэффициент асимметрии, коэффи­циент эксцесса и начальный момент шестого порядка.

5.191. Случайная величина X подчиняется распреде­лению Вейбулла с параметрами п, а, b > 0. Вычислить математическое ожидание и моду распределения.

5.192*. Случайная величина X подчиняется бета-распре­делению с параметрами а > 0 и b > 0. Вычислить матема­тическое ожидание и дисперсию.

5.93*. Случайная величина X распределена по закону Г (а, b). Найти т_X, D_X, a_X, е_X.

5.94*. Случайная величина X распределена по закону χ² (4). Вычислить т_X, D_X и h_X. Критической точкой какого порядка является значение т_X?