Решение типовых задач

Задача 1. Построить функцию распределения U индикатора события А, вероятность которого равна р.

Решение.

 

где q = 1 – p (рис. 5.2)

 

рис. 5.2

Задача 2. В нашем распоряжении имеется n лампочек; каждая из них с вероятностью р имеет дефект. Лампочка ввинчивается в патрон и включается ток; при включении тока дефектная лампочка сразу же перегорает, после чего заменяется другой. Рассматривается случайностная величина Х – число лампочек, которое будет испробовано. Построить ряд ее распределения и найти ее математическое ожидание m_x.

Решение. Ряд распределения величины Х имеет вид

 

где q = 1 – p

Задача 3. Искусственный спутник Земли, движущийся по орбите в течении п суток, может случайным образом сталкиваться с метеоритами. Метеориты, пересекающие орбиту и сталкивающиеся со спутником, образуют стационарный пуассоновский поток с интенсивностью (метеоритов в сутки). Метеорит, попавший в спутник, пробивает его оболочку с вероятностью . Метеорит, пробивший оболочку, с вероятностью выводит из строя аппаратуру спутника. Найти вероятности следующих событий:

А = {за время полета спутника его оболочка будет пробита};

В = {за время полета спутника его аппаратура будет выведена из строя};

С = {за время полета спутника будет пробита только оболочка спутника, а аппаратура будет действовать}.

Решение. Математическое ожидание числа метеоритов, пробивающих оболочку, 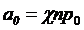. Математическое ожидание числа метеоритов, пробивающих оболочку и поражающих аппаратуру .

; ;

.

Задача 4. Производится ряд попыток включить двигатель. Каждая попытка заканчивается успехом (включением двигателя) с вероятностью р = 0,6. Каждая попытка занимает время . Найти распределение общего времени Т, которое потребуется для запуска двигателя, его математическое ожидание и дисперсию.

Решение. Число произведенных попыток Х есть величина, распределенная по геометрическому закону, начинающемуся с единицы (5.4.10); 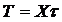имеет распределение

 

(q =1 - p).

Задача 5. Для сборки прибора требуется иметь 4 одинаковые детали; всего в нашем распоряжении 10 деталей, из которых 6 доброкачественных и 4 негодных; на вид детали неразличимы. Из имеющихся деталей выбирают 5 деталей (одну лишнюю «в запас»). Найти вероятность того, что не менее четырех из них окажутся доброкачественными.

Решение. Случайная величина Х – число доброкачественных деталей среди 5 выбранных – имеет гипергеометрическое распределение с параметрами 5, 6, 4. Вероятность того, что среди 5 деталей m будут доброкачественными, равна ; отсюда

 

Задачи.

5.1. Из урны, содержащей три белых и пять черных шаров, наугад извлекают три шара. Пусть Х – число вытянутых черных черных шаров. Построить ряд распределения члучайной величины и найти ее математическое ождидание.

1. Какие значения может принимать величина Х?

2. Чему равны вероятности возможных значений и какому условию удовлетворяет их сумма?

5.2. В группе из десяти издделий имеется одно бракованное. Чтобы его обнаружить, выбирают наугад одно изделие за другим и каждое вынутое проверяют. Построить ряд распределения и найти математическое ожидание и дисперсию числа проверенных изделий.

1. Какие два события должны иметь место, чтобы случайна величина Х (число проверенных изделий) приняла значение 2? Чему равна вероятность Р (Х = 2)?

2. Какие три события должны иметь место, чтобы случайна величина Х приняла значение 3 и т.д.? Чему равна вероятность Р (Х = 3)?

5.3. Два стрелка стреляют по одной мишени, делая независимо друг от друга по два выстрела. Вероятность попадния в мишень для первого стрелка равна 0,5; для второго – 0,6. Построить ряд распределения случайно величины Х – общего числа попаданий и найти ее характеристики m_x и D_x.

1. Какие возможные значения может принимать случайная величина Х?

2. Какие события должны иметь место, чтобы случайна величина Х приняла значение 3, и чему равна вероятность Р (Х = 3)?

5.4. Рабочий обслуживает п однотипных станков, расположенных в ряд с равными промежутками а. Закончив обслуживание какого-либо станка, рабочыий отходит к тому станку, который раньше других потребовал обслуживания. Предполагая, что неполадки в любом из п станков равновероятны, вычислить среднее значение длины перезода рабочего.

1. Длина возможного перехода рабочего является случайной величиной Х. Чему равны возможные значения случайной величины Х?

2. Имея ввиду, что рабочий равновероятно мог находиться у любого из n станков, определить вероятности возможных значений случайной величины Х.

Указание. При вычислении указанных вероятностей необходимо применить формулу полной вероятности, рассматривая гипотезы о том, что рабочий равновероятно находился у i -го станка.

5.4. Охотник, имеющий пять патронов, стреляет в цель до первого попадания (или пока не израсходует все патроны). Найти математическое ожидание и дисперсию числа израсходованных патронов. Построить график функции распределения этой случайной величины, если вероятность попадания при каждом выстреле равна 0,4.

1. Каковы возможные значения случайной величины Х – числа израсходованных патронов и чему равны соответствующие вероятности?

2. Какие точки являются точками разрыва функции распределения и чему равна величина скачка в точке разрыва функции?

5.5. Два стрелка стреляют по одной мишени, делая независимо друг от друга по два выстрела. Вероятность попадания в мишень для первого стрелка равна 0,4, для второго – 0,5.

Пусть Х – число попаданий в мишень первым стрелком, Y – число попаданий в мишень вторым стрелком. Требуется построить ряд распределения случайной величины Z = X – Y и найти ее характеристики m_z и D_z.

5.6. Партия, насчитывающая 50 изделий, содержит шесть бракованных. Из всей партии случайным образом выбрано пять изделий. Требуется построить ряд распределения и найти математическое ожидание числа бракованных изделий, содержащихся в случайной выборке.

5.7. Автоматическая линия при нормальной настройке может выпускать бракованное изделие с вероятностью р. Переналадка линии производится сразу же после выпуска первого бракованного изделия. Требуется построить ряд распределения и найти математическое ожидание и дисперсию числа всех изделий, изготовленных между двумя переналадками линии.

5.8. Рабочий обслуживает четыре станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,7, для второго – 0,75, для третьего – 0,8, для четвертого – 0,9. Построить ряд распределения и найти математическое ожидание и дисперсию числа станков, которые не потребуют внимания рабочего в течение часа.

5.9. Монету подбрасывают шесть раз. Составить ряд распределения и построить функцию распределения отношения числа появления герба к числу появления цифры.

5.10. На пути движения автомобиля шесть светофоров, каждый из них либо разрешает, либо запрещает дальнейшее движение автомобиля с вероятностью 0,5. Составить ряд распределения и построить функцию распределения числа светофоров, пройденных автомобилем до первой остановки. Чему равны математическое ожидание и дисперсия этой случайной величины?

5.11. Имеется шесть ключей, из которых только один подходит к замку. Составить ряд распределения числа попыток при открывании замка, если испробованный ключ в последующих опробываниях не участвует. Чему равны математическое ожидание и дисперсия этой случайной величины?

5.12. Вероятность изготовления нестандартной детали равна 0,1. Из партии контролер берет деталь и проверяет ее качество. Если она оказывается нестандартной, дальнейшие испытания прекращаются, а партия задерживается. Если деталь окажется стандартной, то контролер берет следующую и т.д. Но всего он проверяет не более пяти деталей. Составить ряд распределения числа проверяемых стандартных деталей. Вычислить математическое ожидание и дисперсию этой случайной величины.

5.13. Батарея состоит из трех орудий. Вероятность попадания в цель при одном выстреле из первого, второго и третьего орудия батареи равна соответственно 0,5; 0,6 и 0,8. Каждое из орудий стреляет по некоторой цели один раз. Найти закон распределения числа Х попаданий в мишень. Вычислить математическое ожидание и дисперсию случайной величины Х.

5.14. В ящике лежат n изделий, одно из них бракованное. Из ящика извлекают одно изделие за другим до тех пор, пока не будет вынуто бракованное изделие. Составить ряд распределения числа вынутых изделий. Найти математическое ожидание и дисперсию этой случайной величины.

5.15. Из урны, содержащей пять белых и три черных шара, последовательно вынимают шары, причем операция извлечения продолжается до появления белого шара. Составить ряд распределения числа извлеченных черных шаров и вычислить математическое ожидание и дисперсию, если известно, что: а) вынутые шары в урну не возвращаются; б) вынутые шары возвращаются в урну.

5.16. Два стрелка стреляют поочередно по мишени, причем стрельба ведется до первого попадания. Найти закон распределения числа Х произведенных выстрелов, если известно, что при одном выстреле вероятность попадания доля первого стрелка равна р₁, а для второго – р₂.

5.17. Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения: х₁ – с вероятностью р₁ =0,4 и х₂ (причем х₁ < х₂), если известны математическое ожидание M [ X ]=3,2 и дисперсия D [ X ]=0,96.

5.18. Монета бросается 3 раза. Случайная величина X — число вы­павших гербов. Построить для нее 1) ряд распределения; 2) много­угольник распределения; 3) функцию распределения. Найти М [ X ], D [ X ], .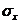

5.19. Рассматривая неслучайную величину а как частный случай
случайной, построить для нее 1) ряд распределения; 2) функцию
распределения; 3) найти ее математическое ожидание и дисперсию.

5.20. К случайной величине Х прибавили постоянную, неслучайную величину а. Как от этого изменятся ее характеристики 1) математическое ожидание; 2) дисперсия; 3) среднее квадратическое отклонение; 4) второй начальный момент?

5.21. Случайную величину X умножили на а. Как от этого изменятся ее характеристики: 1) математическое ожидание; 2) дисперсия;
3) среднее квадратическое отклонение; 4) второй начальный момент?

5.22. Монета подбрасывается n раз; рассматривается случайная ве­личина X — число выпавших гербов. Построить ряд распределения этой случайной величины и найти ее характеристики: т_х, D _х, а_х, .

5.23. Производится n независимых опытов, в каждом из которых с вероятностью р появляется событие А. Написать ряд распределения случайной величины X — числа появлений противоположного А со­бытия в n опытах — и найти ее математическое ожидание и диспер­сию.

5.24. Производится п независимых опытов, в каждом из которых с вероятностью р появляется событие А. Рассматривается случайная величина R — частота появления события А в п опытах, т. е. отно­шение числа появлений события А в п опытах к общему числу про­изведенных опытов п. Написать ряд распределения этой случайной величины; найти ее математическое ожидание и дисперсию.

5.25*. Производится п независимых опытов. Вероятность появления события А во всех опытах одна и та же и равна р. Найти наивероятнейшее число т* появлений события А.

5.26. Два стрелка стреляют каждый по своей мишени, делая неза­висимо друг от друга по одному выстрелу. Вероятность попадания в мишень для первого стрелка p₁, для второго р₂. Рассматриваются две случайные величины: Х₁ — число попаданий первого стрелка; Х₂ — число попаданий второго стрелка и их разность Z = Х₁ — Х₂. Постро­ить ряд распределения случайной величины Z и найти ее характерис­тики m_z и D_z.

5.27. Производится 2 независимых выстрела по мишени. Вероят­ность попадания при каждом выстреле равна р. Рассматриваются слу­чайные величины: X — разность между числом попаданий и числом промахов; Y — сумма числа попаданий и числа промахов. Построить
для каждой из случайных величин X, Y ряд распределения. Найти их
характеристики: т_х, D_х, т_y, D_y.

5.28. Случайная величина Х имеет распределение Пуассона с ма­тематическим ожиданием а = 3. Построить многоугольник распреде­ления и функцию распределения случайной величины X. Найти: 1) вероятность того, что случайная величина X примет значение меньшее, чем ее математическое ожидание; 2) вероятность того, что величина X примет положительное значение.

5.29. При работе ЭВМ время от времени возникают неисправно­сти (сбои). Поток сбоев можно считать простейшим. Среднее число сбо­ев за сутки равно 1,5. Найти вероятности следующих событий:

А = {за двое суток не будет ни одного сбоя};

В = {в течение суток произойдет хотя бы один сбой};

С = {за неделю работы машины произойдет не менее трех сбоев}.

5.30. При заданном положении точки разрыва снаряда цель ока­зывается накрыта однородным пуассоновским полем осколков с интенсивностью λ = 2,5 оск/м². Площадь проекции цели на плоскость, на которой наблюдается осколочное поле, равна S = 0,8 м². Каждый ос­колок, попавший в цель, поражает ее с полной достоверностью. Най­ти вероятность того, что цель будет поражена.

5.31. Та же задача, но каждый осколок, попавший в цель, поражает ее не с полной достоверностью, а с вероятностью 0,6.

5.32. Электронная лампа работает исправно в течение случайно­
го времени Т; после отказа ее немедленно заменяют новой. Поток от­казов — простейший, с интенсивностью μ. Найти вероятности следующих событий: А = {за время τ лампу не придется заменять}; В = {лампу придется заменять ровно три раза};

С = {лампу придется заменять не менее трех раз}.

5.33. Техническое устройство состоит из трех узлов; в первом узле п₁ элементов, во втором п₂ элементов, в третьем n₃ элементов. Первый узел безусловно необходим для работы устройства; второй и третий дублируют друг друга. Потоки отказов элементов — простейшие; для элемента, входящего в первый узел, интенсивность потока отказов равна λ₁, во второй или третий узел λ₂. Первый узел выходит из строя, если в нем отказало не менее двух элементов. Второй узел (так же, как и дублирующий его третий) выходит из строя при отказе хотя бы од­ного элемента. Для выхода из строя устройства в целом достаточно, чтобы отказал первый узел или второй и третий вместе. Найти вероят­ность того, что за время τ устройство выйдет из строя.

5.34. Охотники, собравшиеся для охоты на волка, выстраиваются в цепь случайным образом так, что образуют на оси Ох простейший по­ток точек с интенсивностью λ (λ охотников на единицу длины, см. рис. 5.3). Волк бежит перпендикулярно цепи. Любой охотник стре­ляет по волку только в случае, если волк пробегает от него не дальше чем на расстоянии R₀, и, выстрелив, убивает его с вероятностью р. Определить вероятность того, что волк будет убит, если он не знает, где расположены охотники, и цепь достаточно длинна для того, чтобы волк с достоверностью не пробежал за пределами цепи.

 

рис. 5.3

5.35. Автомашина проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время техосмотра, подчине­но закону Пуассона с параметром а. Если неисправностей не обнаружено, техническое обслуживание машины продолжается в среднем 2 ч. Если обнаружены одна или две неисправности, то на устранение каж­дой из них тратится в среднем еще полчаса. Если обнаружено больше двух неисправностей, то машина ставится на профилактический ре­монт, где она находится в среднем 4 ч. Определить закон распределе­ния среднего времени Т обслуживания и ремонта машины и его мате­матическое ожидание М [ Т ].

5.36*. Обследуется группа животных; каждое из них с вероят­ностью р является больным. Обследование производится путем анали­за крови. Если смешать кровь п животных, то анализ этой смеси будет положительным, если среди п животных будет хотя бы одно больное. Требуется обследовать большое число N животных. Предлагается два способа обследования:

1) обследовать всех N животных; в этом случае нужно провести N

анализов;

2) вести обследование по группам, смешав сначала кровь группы
из п животных; если анализ отрицательный, считать, что все живот­
ные группы здоровы, и переходить к следующей группе из п животных;
если анализ положительный, обследовать каждое из п животных и
после этого переходить к следующей группе (п > 1).

Определить, какой способ обследования выгоднее — первый или второй — в смысле минимального среднего числа анализов. Опреде­лить, при каком п = п* для обследования группы животных потре­буется в среднем наименьшее число анализов.

5.37. Производится ряд зависимых попыток включить двигатель. p_i — вероятность включения двигателя после i — 1 неудачных попыток — есть некоторая функция i: p_i = φ (i). Найти распределение случай­ной величины Т = τХ.

5.38. При сборке прибора повышенной надежности, состоящего из однородных деталей, каждая деталь подвергается всесторонним ис­пытаниям, в результате которых она либо признается доброкачест­венной (с вероятностью р)либо выбраковывается (с вероятностью q = 1- р). Детали оказываются принадлежащими к той или другой категории независимо друг от друга. Запас деталей практически неог­раничен. Отбор деталей и их испытания ведутся до тех пор, пока не будет набрано k высококачественных деталей. Случайная величина X — число выбракованных деталей. Найти распределение случайной величины X: Р_т = Р {X = т }.

5.39. Две случайные величины X, Y независимо друг от друга при­нимают значения 0 или 1. Их ряды распределения заданы:

Построить ряды распределения: 1) их суммы Z = X + Y; 2)их раз­ности U = X - Y; 3) их произведения V = XY.

5.40. Случайная величина X имеет ряд распределения

Построить ряд распределения случайной величины Y = 1/ (3 — X).

5.41. Случайная величина X имеет ряд распределения

Построить ряд распределения ее квадрата: Y = Х ².

5.42. При передаче сообщения по радиоканалу наблюдаются поме­хи, препятствующие декодированию сообщения; с вероятностью р сообщение не удается декодировать. Сообщение передается до тех пор, пока оно не будет декодировано. Продолжительность передачи сообщения равна 2 мин. Найти: 1) математическое ожидание времени Т, которое уйдет на передачу сообщения; 2) вероятность того, что на передачу сообщения понадобится время, большее чем t₀, имеющееся в нашем распоряжении.

5.43. Дискретная случайная величина X имеет распределение

Случайная величина Z есть минимальное из двух чисел — значения случайной величины X и числа а: Z = min { X, а },где х₁ а х_п. Найти распределение случайной величины Z.

5.44. Распределение дискретной случайной величины X есть

Найти распределение случайной величины Z = min { X, 4}.

5.45. Две случайные величины X и Y независимо друг от друга принимают значение согласно рядам распределения:

Построить ряд распределения случайной величины Z = min { X, Y }.

5.46. В условиях предыдущей задачи найти распределение слу­чайной величины U = max { X, Y }.

5.47. В ячейке ЭВМ записано n -разрядное двоичное число; каждый
знак этого числа, независимо от остальных, принимает с равной вероятностью значение 0 или 1. Случайная величина X — число знаков
«1» в записи двоичного числа. Найти вероятности событий {X = т },
{Х т }, { Х < т }.

5.48. Рассматривается правильная десятичная дробь X с тремя
знаками после запятой, причем каждый знак, независимо от других,
с одинаковой вероятностью может принимать любое значение 0, 1,...
..., 9. Построить ряд распределения случайной величины X и найти
ее математическое ожидание.

5.49. Случайная величина Y — случайная двоичная правильная дробь с п знаками после запятой; каждый знак, независимо от других, с вероятностью 1/2 принимает значение «0» или «1». Найти распреде­ление случайной величины Y и ее математическое ожидание М [ Y ].

5.50. Передаваемое по каналу связи в двоичном коде сообщение состоит из последовательности знаков «0» и «1», чередующихся с рав­ной вероятностью и независимо друг от друга, например 0, 0, 1, 1, 1, 0, 1, 1, 1,0,0,0,0, 1,0, 1, 1, 1,...

Рассматривается какая-то группа повторяющихся знаков, напри­мер: 0, 0, 0 или 1, 1, 1, 1 (или просто 0 или 1, если знаки не повторя­ются). Берется какая-то из этих групп наугад. Случайная вели­чина X — число знаков в группе. Найти ее распределение, математи­ческое ожидание и дисперсию. Найти Р { X k }.

5.51. В условиях предыдущей задачи Р {«0»} = 0,7; Р {«1»} = 0,3. Найти среднее число знаков М [ X ] в группе нулей, среднее число знаков М [ Y ]в группе единиц и полное среднее число знаков М [ Z ]в наугад выбранной группе знаков. Найти дисперсии D [ X ], D [ Y ], D [ Z ].

5.52. Техническое устройство (ТУ) состоит из т блоков типа I и
n блоков типа II. Надежность (вероятность безотказной работы в течение заданного времени τ) каждого блока типа I равна р₁, каждого
блока типа II равна р₂. Блоки отказывают (выходят из строя) независимо друг от друга. Для работы ТУ достаточно, чтобы в течение времени τ работали безотказно любые два блока типа I и одновременно
с этим любые два блока типа II. Найти вероятность P безотказной
работы ТУ.

5.53. Прибор применяется (приводится в действие) несколько раз
до его выхода из строя (вышедший из строя прибор не восстанавли­вается). Вероятность того, что, будучи применен k раз, прибор еще не
вышел из строя, равна Р (k). Функция Р (k) задана (см. рис. 5.4).
Известно, что прибор выдержал уже n применений. Найти вероятность
Q_m того, что он выдержит еще т применений, и математическое ожидание числа X будущих применений.

рис. 5.4

5.54. Рабочий обслуживает n однотипных станков, расположенных на одной линии с интервалами l (рис. 5.5). Время от времени станки (с равной вероятностью и независимо друг от друга) останавливаются и требуют наладки. Закончив наладку одного станка, рабочий остается на месте, пока не остановится какой-либо из станков; тогда он пере­ходит к нему (если вышел из строя тот же станок, он остается на мес­те). Случайная величина X — расстояние, которое проходит рабочий между двумя наладками. Найти математическое ожидание случайной величины X.

рис. 5.5

5.55. Производится ряд независимых опытов, в каждом из которых событие А появляется с вероятностью р; опыты ведутся до первого по­явления события А, после чего пре­кращаются. Случайная величина Х - число произведенных опытов. Пост­роить ее ряд распределения и много­угольник распределения; вывести формулы для ее математического ожи­дания, дисперсии, среднего квадратического отклонения.

5.56.. Производится ряд попыток наладить сложную электронную схему. Вероятность того, что схема будет налажена с первой попытки, равна Р₁; со второй попытки Р₂,..., с k -й попытки P_k,... Вероятности P₁, Р₂,..., Р_k,..., Р_п заданы. После п-й безуспешной попытки нала­дить схему попытки прекращаются. Найти математическое ожидание и дисперсию случайной величины X — общего числа произведенных попыток.

5.57. Прибор собирается из деталей k типов; в его состав входят m_i деталей типа i (i = 1,..., k)( m — общее число деталей).

Вероятность того, что наугад взятая деталь i -го типа имеет дефект, равна q_i. Прибор работает только если в составе его деталей нет ни одной дефектной. 1) Найти вероятность Р того, что прибор будет ра­ботать; 2) найти вероятность R₂ того, что среди деталей будет не менее двух дефектных.

5.58. По каналу связи передается k сообщений, содержащих соответственно n₁, n₂,..., n_k двоичных знаков («0» или «1»). Знаки принимают значение 0 или 1 независимо друг от друга и с вероятностью 0,5.
Каждый знак искажается (заменяется противоположным) с вероятностью р. При кодировании сообщений применяется код, исправляющий
ошибки в одном или двух знаках (практически с полной достоверностью). Наличие ошибки хотя бы в одном знаке (после исправления)
делает ошибочным все сообщение. Найти вероятность R того, что
хотя бы одно из k сообщений будет ошибочным.

5.59. Имеется 7 радиоламп, среди которых 3 неисправные, на вид неотличимые от новых. Наугад берутся 4 радиолампы и вставляются в 4 патрона. Найти и построить (в виде многоугольника распределения) ряд распределения числа радиоламп Х, которые будут работать. Найти ее математическое ожидание, дисперсию и среднеквадратическое отклонение.

5.60*. Производится ряд независимых опытов, в каждом из кото­рых событие А появляется с вероятностью р. Наша цель — получить событие A k раз. Максимально возможное число опытов равно n (при­чем n 2 k). Опыты прекращаются либо тогда, когда событие А уже появилось k раз, либо тогда, когда ясно, что уже нет возможности по­лучить его k раз, т. е. когда противоположное событие появилось n - k + 1 раз. Случайная величина X — число опытов, которое бу­дет произведено. Найти распределение случайной величины X.

5.61. В условиях предыдущей задачи п = 7, k = 3; р = 0,4. По­строить ряд распределения случайной величины X.

5.62. Производится один опыт, в результате которого событие А может появиться с вероятностью р и не появиться с вероятностью q = 1 – р. Пусть X — индикаторная случайная величина — принимает значение 1, если событие А произошло, и значение 0, если событие А не имело места. Описать закон распределения случайной величины X, функцию распределения, вычислить математическое ожи­дание, дисперсию, третий центральный момент и определить значение вероятности р, при которой дисперсия макси­мальна.

5.63. Доказать, что для дисперсии случайной вели­чины X справедлива формула .

5.64. а) Выразить центральный момент, n -го порядка через начальные моменты n -го и меньших порядков.

б) Выразить начальный момент n -го порядка через цент­ральные моменты п -го и меньших порядков и математиче­ское ожидание.

5.65. Один раз брошены две одинаковые игральные кости.
Случайная величина S — сумма очков на верхних гранях
игральных костей. Вычислить среднее значение суммы выпавших очков и моду. Вычислить порядок р критической точки χ_p = 10.

5.66. Один раз брошены три одинаковые игральные кости. Случайная величина X принимает значение 1, если хотя бы на одной игральной кости выпадет цифра шесть; принимает значение 0, если шестерка не выпала ни на
одной грани, но хотя бы на одной из граней – появилась цифра 5, и принимает значение —1 в остальных случаях. Описать закон распределения случайной величины X, вы­числить функцию распределения и найти математическое ожидание и моду распределения.

5.67*. Случайная величина X принимает только целые неотрицательные значения. Доказать, что

.

5.68. Из урны, содержащей 4 белых и 6 черных шаров,
случайным образом и без возвращения извлекается 3 шара. Случайная величина Х – число белых шаров в выборке. Описать закон распределения и найти математическое ожидание, моду и дисперсию случайной величины Х.

5.69. Случайная величина X распределена по закону
равнобедренного треугольника в интервале (— а, а) (закону Симпсона), если она непрерывного типа и ее плотность распре­деления вероятностей имеет вид, изображенный на рис. 5.6

рис. 5.6

Написать выражение для f_Х(x), вычислить функцию, распределения вероятностей, математическое ожидание, дисперсию, моду, медиану, коэффициент эксцесса.

5.70. Известно, что при стрельбе по плоской мишени в неизменных условиях случайная величина R — расстоя­ние от точки попадания до центра мишени — подчиняется закону распределения Рэлея с плотностью распределения вероятностей

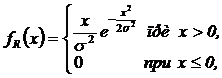
где σ > 0 – параметр, характеризующий распределение. Построить эскиз графика плотности вероятности f_R (x), проверить условие нормировки, вычислить характеристики m_R, D_R, d_R, h_R, a_R и выяс­нить взаимное расположение характеристик m_R, d_R и h_R.

5.71. Скорость V молекул идеального газа, находяще­гося в равновесии при определенной температуре, является случайной величиной, подчиняющейся закону распределения Максвелла с плотностью распределения вероятностей

,

где параметр распределения β > 0 определяется темпера­турой и массой молекул. Выразить среднее значение и наи­более вероятное значение скорости молекул, а также диспер­сию распределения через физический параметр β.

5.72. Случайная величина X подчиняется закону арксинуса с плотностью распределения вероятностей

 

Найти функцию распределения и вычислить т_Х, D_Х, d_Х, h_Х и χ_0,75.

5.73. Случайная величина X непрерывного типа распре­делена по закону Лапласа с параметрами m R и σ > 0, если ее плотность распределения вероятностей задается формулой

.

Выразить характеристики т_Х, е_Х и σ _Х через параметры рас­пределения и изобразить график функции плотности для двух значений параметра σ: σ = σ₂ и σ = σ₁ (σ₁ < σ₂ < ) при одном и том же значении т.

5.74. Аппаратура состоит из 1000 элементов, каждый из которых независимо от остальных выходит из строя за время Т с вероятностью р = 5 * 10⁴. Найти вероятности следующих событий: А = {за время Т откажет хотя бы один элемент}, В = {за время Т откажет ровно 3 элемента},
С = {за время Т откажет не более 3 элементов}.

5.75. Случайная величина X — число электронов, вылетающих с нагретого катода электронной лампы в тече­ние времени t, — подчиняется распределению Пуассона с па­раметром λ t (λ— среднее число электронов, испускаемых в единицу времени). Определить вероятности следующих
событий: А = {за время t₁ число испускаемых электронов
будет меньше m, m N }, В = {за время t₂ вылетит четное
число электронов}.

5.76*. Среднее число вызовов, поступающих на АТС в минуту, равно 120. Найти вероятности следующих собы­тий: A = {за две секунды на АТС не поступит ни одного вызова}, В = {за две секунды на АТС поступит менее двух вызовов}, С = {за одну секунду на АТС поступит хотя бы один вызов}, D = {за три секунды на АТС поступит не менее 6 вызовов}.

5.77. Радиостанция ведет автоматическую передачу цифрового текста в течение 10 мкс. Работа ее происходит при наличии хаотической импульсной помехи, среднее число импульсов которой в одну секунду составляет 10⁴. Для срыва передачи достаточно попадания k импульсов помехи в период работы станции. Считая применимым закон редких
явлений, вычислить вероятность p_k срыва передачи при
значениях k = 1, 2, 3.

5.78. Корректура в 500 страниц содержит 1300 опечаток.
Считая применимым закон Пуассона, найти наиболее вероятное число опечаток на одной странице текста и вероят­ность этого числа.

5.79. Число элементарных частиц, регистрируемых при­бором, случайно и образует пуассоновскую случайную ве­личину со средним значением п частиц. Каждая регистри­руемая частица может нести заряд с вероятностью р и быть нейтральной с вероятностью 1 — р. Определить закон рас­пределения числа заряженных частиц, регистрируемых при­бором, и найти среднее значение и дисперсию полученного распределения.

5.80*. При испытании легированной стали на содержа­ние углерода вероятность того, что в случайно взятой пробе процент углерода превысит допустимый уровень, равна р = 0,01. Считая применимым закон редких явлений, вы­числить, сколько в среднем необходимо испытать образ­цов, чтобы с вероятностью р = 0,95 указанный эффект на­блюдался по крайней мере k раз. (Рассмотреть случаи k = 1,2,3.)

5.81. Для стрелка, выполняющего упражнение в тире, вероятность попасть в «яблочко» при одном выстреле не зависит от результатов предшествующих выстрелов и равна р = 1/4. Спортсмен сделал 5 выстрелов. Найти вероятности событий: А = {хотя бы одно попадание}, В = {ровно одно попадание}, С = {ровно два попадания}, D = {не менее трех попаданий}.

5.82. Пара одинаковых игральных костей бросается 7 раз. Какова вероятность следующих событий: А = {сумма очков, равная 7, выпадет дважды}, В = {сумма очков, равная 7, выпадет по крайней мере 1 раз}, С = {каждый раз выпадет сумма очков, большая 7}, D = {ни разу не
выпадет сумма очков, равная 12}.

5.83. Доказать рекуррентную формулу для биномиальных вероятностей:

и с ее помощью установить, что наиболее вероятное число успехов (d_Х = М)в серии п независимых испытаний удо­влетворяет неравенству

пр — q M < пр + р.

5.84. Два равносильных шахматиста договорились сыграть матч из 2 n результативных партий. Ничьи не учитываются и считается, что каждый из участников может вы­играть очередную партию с вероятностью 0,5. Выигравшим матч считается тот, кто победит в большем числе партий.
В каком матче больше шансов выиграть любому из участ­ников: в матче из 8 результативных партий или из 12?

5.85. Десять осветительных лампочек для елки включены в цепь последовательно. Вероятность для любой лампочки перегореть при повышении напряжения в сети равна 0,1. Определить вероятность разрыва цепи при повышении напряжения в сети.

5.86. Вероятность отказа каждого прибора при испы­тании не зависит от отказов остальных приборов и равна 0,2. Испытано 9 приборов. Случайная величина X — число отказавших за время испытаний приборов. Найти моду распределения d_X и вычислить с четырьмя верными зна­ками вероятности событий А = { X = 0}, В = { X < 3}, С = { X 6}.

5.87*. Устройство состоит из 8 независимо работающих элементов. Вероятности отказов каждого из элементов за время Т одинаковы и равны р = 0,2. Найти вероятность отказа прибора, если для этого достаточно, чтобы отказали хотя бы три элемента из восьми.

5.88. Производится обстрел учебной цели из орудия.
Вероятность попадания в цель при одном выстреле равна р.
Поражение цели может наступить при k попаданиях (k = 1, 2,...) с вероятностью, равной 1 — t^k (0 < t < 1). Вычис­лить вероятность поражения цели при п выстрелах.

5.89. На контроль поступила партия деталей из цеха.
Известно, что 5 % всех деталей не удовлетворяет стандарту.
Сколько нужно испытать деталей, чтобы с вероятностью
не менее 0,95 обнаружить: а) хотя бы одну нестандартную
деталь; б)* не менее трех нестандартных деталей?

5.90. Опыт состоит в том, что из колоды в 32 карты (начиная с семерок и выше) наудачу и с возвращением из­влекается 10 карт, причем каждый раз записывается результат, извлечения. Опыт повторили 4 раза. Найти вероятности следующих событий: А = {по крайней мере один раз
получено не менее 7 карт одной масти}, В = {ровно два раза получены наборы, не содержащие одной какой-либо масти}, С = {ровно один раз получен набор, не содержащий дам, тузов и королей}.

5.91. Шесть раз бросается правильная монета. Случайная величина X — модуль разности числа появлений герба и числа появлений цифры в данном эксперименте. Вычислить среднее значение, моду и дисперсию случайной величины X.

5.92. Проводятся последовательные испытания по схеме
Бернулли. Вероятность успеха в одном испытании равна р.
Вычислить вероятности следующих событий: А = { k -йпо
счету успех наступит в m -м по счету испытании (m k)},
В = { k -йпо счету успех наступит прежде, чем наберется m неуспехов}, С = {все k успехов в п испытаниях появятся подряд}.

5.93. Испытания по схеме Бернулли с вероятностью успеха р в одном испытании повторяются до тех пор, пока не появится успех, после чего прекращаются. Обозначим X число проведенных испытаний до первого успеха вклю­чительно. Найти m_Х, d_Х и D_Х. (Закон распределения случайной величины X называется геометрическим с парамет­ром р.)

5.94*. Вероятность попадания стрелка в мишень в неиз­менных условиях постоянна и равна р. Стрелку выдаются патроны до тех пор, пока он не промахнется. Обозначим X число выданных стрелку патронов в данном экспери­менте. Найти т_Х, D_Х, d_Х.

5.95. Испытания по схеме Бернулли с вероятностью успеха в одном испытании р повторяются до получения ровно k успехов. Описать закон распределения и найти среднее значение числа проведенных испытаний в данном эксперименте. (Указанное распределение называется «отрицательным биномиальным» с параметрами k N и p > 0.)

5.96. Производится стрельба из орудия по удаляющейся цели. При первом выстреле вероятность попадания равна 0,8, при каждом следующем выстреле вероятность попадания уменьшается в 2 раза. Произведено 4 выстрела. Определить вероятности следующих событий: А = {хотя бы
одно попадание}, В = {ровно одно попадание}.

5.97. Прибор состоит из пяти элементов. Отказ k -го элемента за время Т независимо от остальных элементов происходит с вероятностью p_k = 0,2 + (k — 1) * 0,1. Определить: а) математическое ожидание и дисперсию числа отказавших за время Т элементов; б) вероятность того, что за время Т откажет хотя бы один из элементов прибора.

5.98. В первой урне находится 6 белых и 4 черных
шара, во второй — 4 белых и 6 черных шаров. Из первой
урны наудачу последовательно и с возвращением извлекается по одному шару, причем каждый раз перед очередным извлечением независимо от результата предыдущего испытания из второй урны в первую наудачу переклады­вается один шар. Процедуру повторили дважды. Какова
вероятность наиболее вероятного числа извлеченных из
первой урны белых шаров?

5.99*. Проводятся последовательные независимые испы­тания с двумя исходами, причем вероятность успеха в k- мпо счету испытании равна p_k (q_k = 1 — p_k — вероятность неуспеха). Доказать рекуррентную формулу для вероят­ности осуществления k неуспехов в т испытаниях (следо­вательно, т — k успехов в т испытаниях)

5.100. Используя рекуррентную формулу предыдущей задачи, записать выражение для вероятности осуществления ровно двух успехов в четырех испытаниях с вероятностью успеха в k-м испытании, равной р_k.

5.101*. Имеется три урны с номерами 1, 2, 3. В первой урне 7 белых и 5 черных шаров, во второй — 3 белых и 7 чер­ных шаров и в третьей — 2 белых и 3 черных шара. Из каждой урны наудачу извлекается по одному шару. Найти вероятности событий А = {в выборке будет ровно 2 белых шара}, В = {в выборке будет больше белых шаров, чем черных}.

5.102. Произведено три независимых выстрела по мише­ни в неизменных условиях. Вероятность при одном выстре­ле попасть в «десятку» равна р₁₀ = 0,3, вероятность по­пасть в «девятку» равна р₉ = 0,4, вероятность не попасть ни в девятку, ни в десятку равна р₀ = 1 — р₁₀ — р₉ = 0,3. Найти вероятности следующих событий: А = {в результате трех выстрелов будет набрано не менее 29 очков}, В = {ровно два попадания в «десятку»}, С = {одно попа­дание в «десятку» и одно в «девятку»}.

5.103. Каждый из десяти аспирантов группы случайным образом и независимо от остальных выбирает один из четырех дней наступающей недели (понедельник, вторник, среду или четверг) для работы в библиотеке в отделе теку­щей периодики. Найти вероятности следующих событий:
А = {в понедельник в библиотеку явится один аспирант,
во вторник — два, в среду — три, в четверг — четыре
аспиранта}, В = {все десять аспирантов соберутся в библиотеке в четверг}, С = {пятеро из аспирантов появятся в библиотеке в первые два дня недели и пятеро — в следующие два дня}, D = {в понедельник в библиотеке появятся ровно три аспиранта}.

5.104. Два равносильных шахматиста играют матч из
12 партий. В каждой партии возможно три исхода: = {выиграл первый игрок (проиграл второй)}, = {ничья}, = {выиграл второй (проиграл первый)}. Пусть , . Найти вероятности следующих событий: А = {первый игрок выиграл 3 партии, проиграл 3 партии и остальные свел вничью}, В = {один из игроков выиграл 4 партии и проиг­рал 3 партии}, С = {сыграно 6 результативных партий}.