Глава 5. Одномерные случайные величины

С момента возникновения теории вероятностей ее основной задачей было не изучение вероятностных свойств экспериментов со случайными исходами, а связанных с этими экспериментами числовых величин, которые естественно назвать случайными величинами.

Для того, чтобы лучше осознать связь, существующую между случайными величинами и случайными событиями, начнем с пояснения понятия случайной величины.

Случайной величиной естественно называть числовую величину, значение которой зависит от того, какой именно элементарный исход произошел в результате эксперимента со случайным исходом. Множество всех значений, которая случайная величина может принимать, называют множеством возможных значений этой случайной величины.

Следовательно, для задания случайной величины необходимо каждому элементарному исходу поставить в соответствие число – значение, которое примет случайная величина, если в результате испытания произойдет именно этот исход.

Случайные величины будем обозначать прописными латинскими буквами, снабжая их при необходимости индексами: X, Y ₁, Z _i и т.д., а их возможные значения – соответствующими строчными буквами . В русскоязычной литературе принято также принято также обозначение случайных величин греческими буквами: и т.д.

Рассмотрим примеры.

Пример 5.1. В опыте с однократным бросанием игральной кости случайной величиной является число Х выпавших очков. Множество возможных значений случайной величины Х имеет вид . Если вспомнить, как выглядит пространство элементарных исходов в этом опыте, то будет очевидно следующее соответствие между элементарными исходами и значениями случайной величины Х:

.

Иными словами, каждому элементарному исходу , ставится в соответствие число i.

Пример 5.2. Монету подбрасывают до первого появления «герба». В этом опыте можно ввести, например, такие случайные величины: Х – число бросаний до первого появления «герба» с множеством возможных значений {1,2,3,…} и Y - число «цифр», выпавших до первого появления «герба» с множеством возможных значений {0,1,2,…} {ясно, что Х = Y + 1}. В данном опыте пространство элементарных исходов Ω можно отождествить с множеством , причем элементарному исходу Ц…ЦГ ставится в соответствие число m +1 или m, где m – число повторений буквы «Ц».

Пример 5.3. На плоский экран падает частица. Будем считать, что нам известна вероятность попадания частицы в любое (измеримое, т.е. имеющее площадь) множество на экране. Случайными величинами в данном случае будут, например, расстояние Х от центра экрана до точки падения, квадрат расстояние , угол Z в полярной системе координат и т.д.

Теперь мы можем дать определение случайной величины. Скалярную функцию , заданную на пространстве элементарных исходов, называют случайной величиной, если для любого - множество элементарных исходов, для которых является событием. Для кратности условимся в дальнейшем вместо записи использовать запись , если необходимо подчеркнуть связь случайной величины с пространством элементарных исходов Ω, или даже запись , если не акцентируется внимание на этой связи.

Для исследования вероятностных свойств случайной величины необходимо знать правило, позволяющее находить вероятность того, что случайная величина примет значение из подмножества ее значений. Любое такое правило называют законом распределения вероятностей, или распределением (вероятностей) случайной величины. При этом слово «вероятностей» обычно опускают.

Общим законом распределения, присущим всем случайным величинам, является функция распределения.

Функцией распределения (вероятностей) случайной величины Х называют функцию F (x), значение которой в точке х равно вероятности события , т.е. события, состоящего из тех и только тех элементарных исходов , для которых :

.

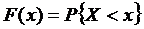Обычно говорят, что значение функции распределения в точке х равно вероятности того, что случайная величина Х примет значение, меньшее х.

Свойства функции распределения:

1.) .

2.) при (F (x) – неубывающая функция).

3.) .

4.)

5.) где непрерывная слева функция).

Можно показать, что любая неубывающая непрерывная слева функция F (x), удовлетворяющая условиям

и ,

является функцией распределения некоторой случайной величины Х.

В некоторых учебниках функцией распределения называют функцию, значение которой в точке х равно вероятности события .Такое определение ничего не меняет в наших рассуждениях. Единственное изменение касается свойства 5: функция F (x) будет непрерывна справа.