Анализ амплитудного метода при регистрации изменения светорассеяния

 

В настоящем разделе представлены результаты теоретического анализа прохождения света из ИЭ в клетки, находящиеся на рабочей поверхности ИЭ-та.

При нанесении клеток на рабочую поверхность ИЭ их морфология оказывается сложной. Поэтому вначале проведем анализ модели - монослоя распластанных клеток (рис. 5.1а).

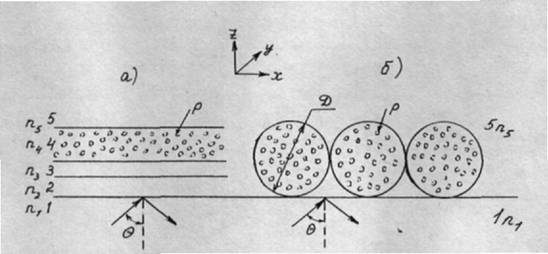
В качестве модели были взяты два крайних случая (рис. 5.1 а и б): а/ структура, состоящая из плоских параллельных слоев, соответствующих зазору между плазматической мембраной и поверхностью стекла, плазматической мембране и цитоплазме; б/ в качестве модели слоя сферических клеток на поверхности стекла рассматривали монослой однородных сфер, внутри которых находятся частицы, рассеивающие световую волну.

В слое, соответствующем цитоплазме, полагали наличие равномерно распределенных рассеивающих световую волну частиц. Считали, что рассеяние описывается либо законом Рэлея, либо законом Рэлея-Ганса. Силу света рассеянной волны определяли как результат однократного рассеяния независимыми частицами. Слои 1, 2, 3, 4, 5 (рис. 5.1а) характеризуются показателями преломления (ПП) n₁, n₂, n₃, n₄, n_5, соответственно. Рассматривали случаи, когда есть зеркальное отражение от верхней границы монослоя (n₄ ≠ n₅) и когда нет отражения (n₄ = n₅) (следствие шероховатости верхней границы).

 

 

Рис. 5.1 а и б.

 

В качестве модели слоя сферических клеток на поверхности стекла рассматривали монослой однородных сфер, внутри которых находятся частицы, рассеивающие световую волну (рис. 5.1б).

Для нахождения интенсивности плоской волны, прошедшей в слой 4, применяется теория матриц слоистых сред, связывающих значение характеристик поля внутри слоя с их значениями на границе.

 

Опуская многочисленные выкладки, результаты численного расчета на ЭВМ представлены графически на рис. 5.2 и рис. 5.3. На основании графического материала сделаем ряд выводов.

 

 

 

Рис. 5.2. Зависимость при НПВО светового потока (Ф) от угла падения θ плоской электромагнитной волны для модели монослоя распластанных клеток (1 - показатель преломления цитоплазмы – 1,36 и 2 – 1,40).

 

 

Теоретические зависимости для модели монослоя распластанных клеток имеют общую особенность, которая не зависит ни от поляризации падающей волны, ни от закона рассеяния. Она заключается в том, что рассеянный световой поток Ф начинает резко уменьшаться при угле θ₂ таком, что sinθ₂ = n₁ /n₄, а не при угле θ₁. Это позволяет определить ПП цитоплазмы, т.к. n₁ известно, а θ₂ определяем в эксперименте. Физический смысл такой зависимости состоит в том, что при θ > θ₂ поле волны в цитоплазме становится экспоненциально затухающим с глубиной проникновения d. Наблюдается эффективное экранирование проникновения волны в клетки практически при всех θ > θ₂.

 

 

Рис. 5.3. Зависимость при НПВО светового потока от угла падения луча

света для моделей распластанных (1) и сферических (2) клеток.

 

 

Кривые на рис. 5.2 при θ > θ₂ имеют линейный участок. Производная на этом участке ∆lnФ / ∆sinθ зависит от поляризации падающей волны, от ширины щели 2, но не зависит от закона рассеяния, ПП среды в зазоре 2, толщины плазматической мембраны. Это позволяет использовать значение производной для оценки зазора между плазматической мембраной и ИЭ, задавая в эксперименте ТЕ-поляризацию падающего луча света.

Кривая 2 на рис. 5.3 для модели монослоя сферических клеток заметно отличается от кривых для модели распластанных клеток. В этом случае резкое уменьшение рассеянного светового потока по мере роста θ начинается с предельного угла ПВО от границы "ИЭ - культуральная среда". По мере возрастания θ от θ₁ до θ₂ световой поток резко уменьшается.

Существенное различие кривых 1 и 2 на рисунках свидетельствует о том, что исследуемая зависимость может дать информацию о кинетике уплощения клеточной поверхности, прилегающей к поверхности ИЭ.

Отметим, что отсутствие значительного изменения рассеянного светового потока при θ < θ₂ в случае модели слоя распластанных клеток является следствием того, что при этих углах волна, прошедшая в слой, соответствующий цитоплазме, является бегущей, а не экспоненциально затухающей, как в среде над монослоем и в зазоре 2. Это означает, что площадь контакта клеток с ИЭ проницаема для бегущей электромагнитной волны в указанном интервале углов, поверхность ИЭ незанятая клетками - непроницаема. Это имеет следующие следствия.

Во-первых, величина уменьшения светового потока при увеличении θ от θ₁ до θ₂ позволяет оценить площадь контакта поверхности клетки с ИЭ. Это следует из того, что световой поток, входящий в слой клеток, будет пропорционален площади контакта клеток в распластанном состоянии S0 и световой рассеянный поток при увеличении θ от θ₁ до θ₂ будет неизменным. В произвольном случае площадь контакта будет оцениваться как S = S0(Ф/Ф0) (Ф - регистрируемый световой поток).

Второе следствие состоит в том, что нахождение поля волны, прошедшей в одиночную распластанную клетку, сводится к задаче о дифракции плоской электромагнитной волны на "отверстии", соответствующем площади контакта клеток с ИЭ, с учетом разницы показателей преломления до "отверстия" и после него.

Изучение представленных на рисунках зависимостей позволяет исследовать кинетику уплощения клеточной поверхности, обращенной к ИЭ. Степень уплощения, а также форму клеточной поверхности охарактеризуем разностью натуральных логарифмов измеренных значений световых потоков ∆lnФ = lnФ(θ₁) - lnФ(θ₂).

Отметим также, что методы, основанные на НПВО, являются прижизненными. Измерения можно проводить, не оказывая на клетки воздействия. Это достигается также и тем, что для выполнения измерений нет необходимости в изменении среды, субстрата.

Методы, основанные на НПВО, позволяют получить параметр, усредненный по популяции клеток (например, при исследовании динамики уплощения клеточной поверхности, обращенной к ИЭ, при оценке площади ее контакта с ИЭ, при измерении усредненного ПП вблизи контакта клеточной поверхности с ИЭ по значению θ₂.

И, наконец, проведенный анализ показал, что, зная глубину проникновения электромагнитного поля в клетки, а также площадь клеток на этой глубине, имеем значение объема прореагировавшего со светом клеточного вещества, что дает возможность проводить количественные измерения, о которых было сказано выше.