Способ диагностики состояния организма по изменению «морфологического портрета»

 

В данном разделе рассмотрим возможность использования спектроскопии внутреннего отражения для получения интегральных динамических морфологических характеристик неоднородных популяций клеток, что дает возможность использовать такие характеристики для оценки физиологическое состояние организмов.

Большое значение для современного естествознания имеет проблема исследования структуры материи (в физике, химии, биологии, механике), ибо структура яв­ляется основой функционирования любой системы, определяя ее физико-химиче­ские, механические и другие свойства. Однако анализ изображений микроско­пических структур чаще всего сводится лишь к визуальной оценке зрительных образов, полученных с помощью разнооб­разной и сложной техники современной микроскопии. В результате значительная часть информации остается нерасшифро­ванной, непрочитанной. Очевидна необходимость максимального ограничения субъективного фактора в за­дачах медицинской диагностики, при оценке воздействии на структуру внешних факторов, возрастной морфологии и во многих технических приложениях (метал­ловедение, петрография, физическая химия и др.). Необходимо также перевооружение теоретической морфологии, нуж­дающейся в количественной оценке, в математическом описании структур. Исследования показали, что статистические характеристики структуры клеточной популяции могут быть с успехом использованы как отличитель­ные признаки ее физиологического состояния. К основным задачам подобного анализа относятся стереологическая реконструкция трехмер­ных надмолекулярных структур по их двумерным изображениям или двумерным спектрам, математическое описание структуры и оценка степени ее упорядоченности с применением средств современной вычислительной техники.

При полном внутреннем отражении (ПВО) электромагнитного излучения на регулярных структурах образуется спе­цифическая картина объ­екта - его объемный спектр. При этом оптическая система осуществляет опера­цию объемного преобразования Фурье для поля распределения плотностей в плоскости объекта.

В основу метода количественного анализа морфологических структур по их стати­стическим характеристикам положен ана­лиз сигнала, полученного при сканировании по глубине исследуемого образца. Образец сканируется оптически (УФ, видимая или ИК области спектра) в режиме нарушенного ПВО (НПВО) по глубине проникновения светового потока за границу поверхности измерительного элемента (ИЭ). Специфичная для каждого состояния клеток фор­ма сканограммы отражается в форме кривой распределения амплитуд. Т.о. форма сканограммы представляет собой обобщенный морфологический портрет клеточной популяции.

Определение объема прореагировавшего со светом вещества построено на частичном нарушении полного внутреннего отражения (ПВО) при изменении углов падения θ, близких к критическому θ_кр. При ПВО излучение выходит за границу раздела двух сред на величину, соизмеримую с длиной волны (λ) этого излучения. Поэтому при подходе θ к θ_кр излучение начнет проходить через зазор в образец, уменьшая величину отраженного светового потока, а форма области оптического контакта (область, где зазор между образцом и отражающей поверхностью ИЭ равен нулю) воспроизводит форму объекта исследования за счет охвата площади оптического контакта и объема вещества. Это означает, что можно иметь информацию о количестве объекта, прореагировавшего со световым потоком, что дает возможность проводить количественную оценку тех или иных параметров вещества в анализируемом слое образца. Для обоснования указанных возможностей предложенного метода нужно показать, что отражательная способность (R) зависит от величины зазора (S), т.к. форма объекта изменяет эту величину. Кроме того, необходим механизм для изменения глубины проникновения света за границу раздела двух сред, что обеспечивает регистрацию изменения зазора от формы объекта.

Проведем этот анализ.

Для плоской (параллельный поток) неполяризованной световой волны отражательная способность R при нарушении ПВО описывается выражением, куда входят коэффициенты отражения для волн света с различной поляризацией:

 

R = 1/2 [ ׀ r_TE ׀ ² + ׀ r_TM ׀ ², (6.1)

 

где r_TE и r_TM – коэффициенты отражения для волн света с ТЕ – и ТМ – поляризацией.

Аналитически эти коэффициенты отражения выражаются с помощью выражения:

 

 

(n₃/n₂)²(a/b) – (n₁/n₂)²(a/c) – ith(KSa)[1 + (n₁n₃/n₂²)²(a²/bc)]

r_{TE (TM)} = ^{__________________________________________________________________________}, (6.2)

(n₃/n₂)²(a/b) + (n₁/n₂)²(a/c) + ith(KSa)[1 - (n₁n₃/n₂²)²(a²/bc)]

 

где а = (n₃²_*sin²θ₃ - n₂²)^1/2,

b = (n₁² - n₃²_* sin²θ₃)^1/2,

с = n₃cosθ₃,

n₁, n₂, n₃ – показатели преломленияИЭ-та, вещества зазора и объекта контроля соответственно,

К_О = 2π/λ_О – волновое число (λ_О – длина волны света в вакууме),

S – величина зазора,

th – гиперболический тангенс.

Как видно, отражательная способность зависит от показателей преломления материала ИЭ-та и объекта исследования, а также от угла падения луча, длины волны света и величины воздушного зазора. При различных формах объектов величина зазора будет неравномерной. Поэтому необходимо проанализировать величину отражательной способности R ИЭ-та.

Известно также, что отражательная способность зависит от показателей преломления материала ИЭ и объекта исследования, а также от угла падения луча, длины волны света и величины воздушного зазора, так как при записи спектральных характеристик в режиме "массивного образца" (при d_р < d, где d_р - глубина проникновения светового потока в образец; d - толщина образца) глубина проникновения светового потока определяется из равенства (для простоты воспользуемся приближенным выражением):

 

 

d_p = λ₁ / [2π (sin²θ – n₂₁²)]¹/², (6.3)

 

 

где n₂₁ = n₂ / n₁ - относительный показатель преломления; n₁ - показатель преломления ИЭ на анализируемой длине волны; n₂ - показатель преломления исследуемого объема на этой же длине волны; λ₁ - длина волны в среде с показателем преломления n₁; θ - угол падения светового потока на рабочую поверхность ИЭ.

Приведенное выражение показывает, что имеется и механизм для изменения глубины проникновения света за границу раздела двух сред, что необходимо для регистрации изменения зазора от формы объекта по его объему.

При различных формах клеток величина зазора будет неравномерной и изменяться в зависимости от соотношения количества клеток с различными формами и размерами. ПО формулам (6.1) и (6.2) был проведен расчет на ЭВМ отражательной способности ИЭ-та, изготовленного из материала КО-5, для коллимированного и монохроматиченого луча света. Результаты расчета показывают, что при изменении углов падения θ изменение отражательной способности R пропорционально величине относительного зазора, т.е. форме и размерам объекта изучения.Проверим это.

Будем считать, что на рабочую поверхность ИЭ нанесены интактные клетки самой разнообразной формы и разных размеров, располагающиеся на расстоянии, когда начальная величина зазора S₀ ≤ λ₀, т.е. на расстоянии менее глубины проникновения светового потока в объекты. Условно выберем одно тело сферической формы с радиусом r_m, расположенное над ИЭ на расстоянии менее глубины проникновения d_p. Если приложить усилие, то объект может изменить форму ("прогнуться"), а в центральной части зазор между рабочей поверхностью ИЭ и объектом уменьшится на какую-то величину U: это эквивалентно тому, что изменилось соотношение между клетками различной формы и размеров. При этом в центре рабочей поверхности ИЭ образуется некоторая область, где зазор меньше глубины проникновения светового потока, и наблюдается выход излучения из ИЭ через зазор в объект, т.е. происходит нарушение ПВО. Это эквивалентно какому-то заполнению рабочей поверхности ИЭ. Если получить значения R для зазора и величин прогиба U центральной части объекта, то эти значения несут информацию о форме объекта, его размерах, т.е. об обобщенном морфологическом портрете объекта.

 

 

Рис. 6.1. Зависимость S/λ_О для различных θ.

 

 

Рассмотрим методику определения формы объекта на частном примере. При различных соотношениях между размерами и формой клеток величина зазора должна быть неодинаковой и зависеть от координаты Х, которая равна величине удаления от центра отражающей поверхности измерительного элемента. При различных соотношениях между размерами и формой клеток величина зазора должна быть неодинаковой и зависеть от величины (Х) удаления от центра эквивалентного тела. Для простоты будем полагать, что поверхность является сферической с радиусом кривизны, который можно определить из соотношения:

 

 

r_m = [ U (2r_k - U)]¹/², (6.4)

 

 

где r_m - радиус объекта;

r_k - радиус кривизны поверхности объекта;

U - величина прогиба относительно центральной части объекта.

Поскольку величина прогиба меньше радиуса кривизны, то приближенно радиус кривизны можно определить следующим образом:

 

r_k = (r_m²/2U). (6.5)

 

Величина зазора между "прогнувшейся поверхностью" и отражающей поверхностью ИЭ связана со значением X следующей зависимостью:

 

Х = {(S - U)[2 r_k - (S - U)]}¹/². (6.6)

 

На рис. 6.2 изображены зависимости R от Х при объектах различного диаметра. Эти зависимости были рассчитаны по формулам (6.4 – 6.6)для случая, когда r_m = 10мм, n = 1,6, θ = 45º, S₀ = 1 мкм. Из расчетов следует, что изменение R таково, что при каждом прогибе (увеличение заполнения ИЭ) в центре рабочей поверхности ИЭ возникает область, где отражательная способность изменяется слабо и ее можно считать постоянной, а ближе к краю объекта она резко возрастает до максимального значения. Поэтому для упрощения дальнейших расчетов, аппроксимируем зависимость отражательной способности ступенчатой функцией и считаем, что в центре образца имеется плоская площадка, перемещение которой равно величине прогиба центра объекта исследования. Диаметр этой площадки равен диаметру сечения сферической поверхности полностью "прогнувшегося" объекта (т.е. полному заполнению рабочей поверхности). Тогда диаметр области оптического контактазапишется следующим образом:

 

Ǿ = 2[0,5λ(2 r_k - 0,5λ)]¹/², (6.7)

 

где Ǿ - диаметр области оптического контакта, r_k - радиус кривизны поверхности прогнутого объекта, λ - длина волны света. Радиус кривизны поверхности объекта можно определить как:

 

r_m = [S₀ (2 r_k – S₀)]¹/², (6.8)

 

где r_m - радиус объекта;

S₀ - начальная величина зазора.

 

 

 

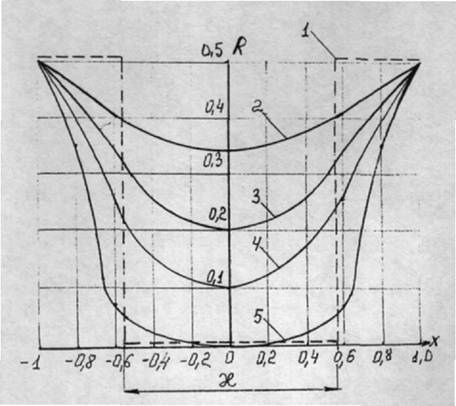
Рис. 6.2. Зависимость R от различных значений U: (1/ U = 0; 2/ U = 0,25 S_O; 3/ U = 0,5 S_O; 4/ U = 0,75 S_O; 5/ U = S_O)

 

 

Пренебрегая величиной S_O и λ_О, ввиду их малости по сравнению с r_k, и подставляя значение r_k из (6.7) в (6,6), получим:

 

Ǿ = r_m[0,4(λ/S₀)]¹/². (6.9)

 

Т. о. показано, форма области оптического контакта зависит от формы объекта изучения, а размеры области оптического контакта (назовем ее так условно, поскольку этот термин обозначает бесклеевое соединение двух оптических деталей, удерживаемых силами межатомного притяжения, возникающее при величине зазора <0,1 доли длины волны света) пропорциональны "деформации" объекта, т.е. зависят от его "уплощения", зависящее от соотношения в образце клеток разных размеров и формы.

Покажем далее, что существует зависимость отражательной способности от площади контакта образца с ИЭ-том.

Если построить зависимости отражательной способности от угла падения для различных показателей преломления ИЭ, рассчитанные по формулам Френеля (для воздуха и образца) (рис. 6.3), то можно определить область углов падения при экспериментальной работе. Штриховой линией обозначена отражательная способность для границы ИЭ-та с воздухом. На этоми же рисунке изображена отражательная способность от границы этого же ИЭ-та с объектом.

 

 

 

Рис. 6.3. Зависимость R от θ для различных показателей преломления n.

 

 

Здесь при расчете отражательной способности не учитывается тот факт, что объект обладает светопоглощением. Если так, то в формулы Френеля необходимо вместо показателя преломления объекта n₁ поставить комплексный показатель преломления:

 

n₁′ = n₁ + i(α·λ/4π), (6.10)

 

где α - показатель поглощения;

λ - длина волны используемого света.

Известно, что если численное значение действительной части показателя преломления объекта значительно превышает значение мнимой части, то влиянием светопоглощения на отражательную способность можно пренебречь. Заметное влияние светопоглощения сказывается лишь при α = 10⁴см‾¹ и только для углов падения, превышающих критический угол ПВО. Световой поток, попадающий внутрь области оптического контакта, полностью поглощается, а минующие эту область лучи света испытывают ПВО вне зависимости от угла падения.

При отсутствии оптического контакта все лучи испытывают ПВО от рабочей поверхности измерительного элемента (отражательная способность R = 1), а при наличии оптического контакта все лучи, попадающие в зону контакта, не распространяются в измерительном элементе (отражательная способность R < 0,05).

На рис. 6.4 приведены теоретические зависимости для монослоя целлюлозы и для слоя сферического латекса.

 

 

Рис. 6.4. Кривые монослоя целлюлозы (1) и сферического латекса (2)

Для экспериментальной проверки теоретического анализа в качестве условного монослоя был выбран монослой целлюлозы и слой клеток цианобактерий Anabaena variabilis.

Особенностью экспериментальных кривых, как и теоретических, является то, что для монослоя сферических частиц резкое возрастание светового потока при возрастании θ начинается с предельного угла ПВО от границы рабочей поверхности «ИЭ-среда 2» (θ₁). Измерение θ₁ проводилось при отсутствии частиц. Для монослоя целлюлозы резкое возрастание R начинается при угле θ₂, превышающим θ₁. Согласно результатам теоретического анализа угол θ₂ связан с показателем преломления монослоя вблизи контактирующей с ИЭ-том поверхностью и позволяет его определить из приведенных выше соотношений.

 

 

 

Рис. 6.5. Экспериментальные зависимости R от θ для монослоя распластанных (1) и «сферических» клеток (2).

 

 

Согласно теоретическому анализу производная d_*lnR/d_*sinθ на линейном участке при θ > θ₂ позволяет оценить расстояние от поверхности измерительного элемента до монослоя.

Резкое различие между экспериментальными данными подтверждает вывод о том, что изучение таких зависимостей позволяет исследовать динамику изменения обобщенного морфологического портрета. Степень изменения можно охарактеризовать разностью натуральных логарифмов измеренных значений световых потоков ∆lnR = lnR(θ₁) - lnR(θ₂). Значение lnR позволяет оценить площадь поверхности, удаленной от поверхности ИЭ на расстояние не более глубины проникновения света в образец, т.е. определить объем прореагировавшего со светом объекта. Например, для сферических частиц площадь контакта (пропорциональная объему) равна:

 

S = S_Oe ^{–πl nR}, (6.11)

 

где S_O – площадь проекции частицы на рабочую поверхность ИЭ-та.

Были проведены и эксперименты, когда рабочую поверхность измерительного элемента заполняли смесью клеток, имеющих разнообразную форму и размеры. Эта смесь не контролировалась в количественном соотношении. О полученных результатах (рис. 6.6) можно сказать следующее.

 

 

 

Рис. 6.6. Экспериментальные зависимости от θ для монослоя (1) и одиночных (2) распластанных клеток.

 

 

На основании вида экспериментальных кривых можно сделать вывод, что по излому измеряемой зависимости можно определить показатель преломления измеряемого объекта. Данный подход позволяет получить усредненный по массе параметр объекта вблизи контакта с ИЭ-том.

Увеличение светового потока начинается также при угле θ₁. Однако, изменение менее резкое в сравнении с зависимостью для сферических частиц. Это означает, что интегральная форма клеток, обращенных к измерительному элементу, отлична от сферической, и что увеличивается площадь (т.е. объем) контакта клеток с измерительным элементом.

Рассмотренный в данном разделе подход при анализе результатов сканирования морфологических объектов на основе методов статистики случайных процессов дает возможность не только определить усредненный параметр культуры – морфологический портрет, не только определить количество того или иного вещества в исследуемом образце, но и решить более важную задачу о структурном распределе­нии данного вещества в клетках, оценить сте­пень перераспределения при патологии и при различных воздействиях, направленных на возврат структуры к норме, и дать количественную оценку степени упорядоченно­сти морфологических структур.