Равносильные логические выражения

Равносильные логические выражения(эквивалентные) т.е если в таблицах последние столбцы совпадают.

Логические функции – функция лог.переменных, которая может принимать два значения 0 и 1. p(X1,X2,X3,...,Xn) – может быть задана таблицей истинности.

Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Логические законы и правила преобразования лог.выражений.

Закон двойного отрицания

Переместительный(коммутативный)закон

Сочетательный(ассоциативный)

Распределительный(дистрибутивный){ (A +B)&C = (A&C)+(B&C)}

Общей инферсии(Морагн) { = & }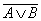

Закон идемпотентности {A&A = A. /A +A = A}

Законы исключения констант {A+1 = 1,A+0 = A}

Закон противоречия {A& = 0}

Закон исключения третьего A Ú = 1

Законпоглощения{A+(A&B) = A/ A&(A Ú B) = A}

Закон исключения(склеивания){ (A&B)+( &B) = B/(A Ú B)&( Ú B) = B}

Закон контрапозиции (правило перевертывания):
┐(А→В) = А&┐В
┐А&(А+В)= ┐А&В
А+ ┐А&В=А+В}

Логические функции.

Таблица истинности, показывает, какие значения, принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.

При построении таблицы истинности принято пользоваться следующим алгоритмом:

Подсчитать количество переменных n в логическом выражении;

Определить количество строк в таблице истинности;

Количество строк m = 2n

Подсчитать количество логических операций в логическом выражении;

Определить количество столбцов в таблице, которое равно количеству логических переменных плюс количество логических операций;

Ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;

Заполнить столбцы входных переменных наборами значений;

Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.