Язык логики предикатов второго порядка 4 страница

Устанавливая отношения между понятиями, важно не отождествлять понятия с общими именами или просто словами, не выражающими понятий. Чтобы избежать такого отождествления, нужно всякий раз выяснять, какие понятия выражают те или иные слова или словосочетания. Пусть, например, требуется установить, в каких отношениях по объемам находятся понятия (1) «стоимость», (2) «потребительная стоимость», (3) «меновая стоимость». На первый взгляд кажется, что объем понятия (1) включает в себя объемы понятий (2) и (3), а понятия (2) и (3) являются несовместимыми между собой, т.е. что два последних понятия находятся в отношении соподчинения к первому. Так ли это на самом деле?

Выявим понятия, вместо которых введены слова «стоимость», «потребительная стоимость», «меновая стоимость». Эти понятия следующие: (1) «Определенное количество общественно необходимого труда, затраченное на производство товара»; (2) «Полезность вещи, ее способность удовлетворять какую-либо человеческую потребность»; (3) «Количественное соотношение, в котором обмениваются товары, как потребительные стоимости».

Эти понятия несовместимы по объемам. Первое понятие - один из видов стоимости наряду с потребительной и меновой. С логической точки зрения для этого (первого) понятия нужно ввести другое название - какая-то специфическая стоимость - и образовать новое понятие, в объем которого войдут объемы всех трех рассмотренных понятий. Сокращением для словесного выражения понятия (4) целесообразно использовать слово «стоимость».

8.5.

§ 5. Операции с объемами понятий (классами), их связь с операциями над содержаниями понятий. Диаграммы Венна

В некоторых случаях возникают затруднения при установлении отношений между понятиями по объемам. Пусть, например, даны понятия «человек такой, что если он мудр, то он философ» и «человек, который является мудрым». В каком отношении по объемам находятся эти понятия?

Для установления вида отношений между понятиями можно объем понятия, содержание которого выражается формулой, включающей логические термины свести к результату применения определенных операций с объемами понятий, содержание которых выражается формулами, не включающими логических терминов.

Основными операциями с объемами понятий (классами) являются: пересечение классов, объединение классов, дополнение к классу.

Пересечением двух классов называется операция, обозначаемая знаком , в результате применения которой к классам WxA(x) и WxB(x) образуется класс , элементами которого являются те и только те предметы, которые входят как в класс WxA(x), так и в класс WxB(x).

На схемах класс представлен заштрихованными поверхностями:

В четвертом случае класс пуст.

Объединением двух классов называется операция, обозначаемая знаком и, в результате применения которой к классам WxA(x) и WxB(x) образуется класс 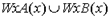, элементами которого являются те, и только те, предметы, которые входят по крайней мере в один из исходных классов.

Графически класс 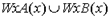представляется заштрихованными поверхностями:

Дополнением к классу (в универсуме) называется операция, обозначаемая знаком , в результате применения которой к классу WxA(x) образуется класс , элементами которого являются те и только те предметы из области значения переменной х (из рода понятия), которые не входят в класс WxA(x). На схеме этот класс представлен заштрихованной поверхностью.

Основными операциями над содержаниями понятий являются: отрицание содержания, конъюнкция содержаний и дизъюнкция содержаний. Между основными операциями над содержаниями понятий и операциями над объемами понятий существует следующая связь:

С использованием языка логики предикатов исследуемые понятия «человек такой, что если он не мудр, то он не философ» и «человек, который является мудрым» можно записать соответственно так:

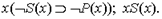
Используя известные связи между логическими терминами:

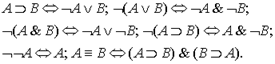
и др., первое понятие можно записать: и

Зная связь между операцией над содержаниями, выражаемой знаком дизъюнкции, и операцией объединения объемов понятий, объем понятия 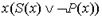заменим классом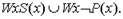

Для установления вида отношения между классами и WxS(x) используем диаграммы Венна. Диаграмма строится так. Универсум рассуждения (род понятия), т.е. область значений переменной х, изображается посредством квадрата. При этом при записи понятий с использованием языка логики предикатов переменная х в записи сравниваемых понятий должна иметь одну и ту же область значений, т.е. можно устанавливать отношения между понятиями, имеющими один и тот же род. В рассматриваемом примере универсумом рассуждения является класс людей.

Далее универсум делится на две части. Одна часть соответствует предметам, входящим в класс WxS(x), а вторая - в дополнение к этому классу.

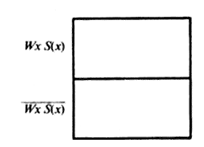
Затем каждая из полученных частей в свою очередь делится на две части, одна из которых соответствует классу WxP(x), а другая - классу .

(Если в записи понятия имеется третий предикат, то деление продолжается - каждая из полученных четырех частей разбивается на две, как показано ниже, и т.д.).

Заштрихуем часть, соответствующую классу WxS(x) и классу .

Классу соответствует вся заштрихованная поверхность схемы, т.е. часть, представляемая квадратами 1, 2 и 4.

Класс WxS(x) представляется заштрихованной поверхность следующей схемы:

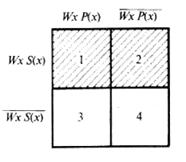
Понятия находятся в отношении подчинения. Первое понятие является подчиняющим, а второе подчиненным.

Установим, в каком отношении находятся понятия (1) «число, которое делится на 2, но не делится на 16» и (2) «число такое что если оно делится на 2, но не делится на 3, то оно делите на 16».

Их записи с использованием языка логики предикатов:

Графическое представление первого понятия:

Объем первого понятия представляется частью схемы, заштрихованной дважды, т.е. прямоугольниками 3 и 4.

Графическое представление второго понятия:

Объем второго понятия представляется всей заштрихованной частью схемы, т.е. прямоугольниками 1, 3, 4, 5, 6, 7, 8.

Понятия находятся в отношении подчинения. Второе понятие является подчиняющим, а первое - подчиненным.

8.6.

§ 6. Обобщение и ограничение понятий

Обобщение и ограничение понятий являются операциями, которые осуществляются на основе закона обратного отношения.

Обобщение понятия - это переход от некоторого понятия к понятию с большим объемом, но меньшим содержанием.

Например, результатом обобщения понятия «млекопитающее животное, обитающее на суше» (А), является понятие «млекопитающее животное» (В), а результатом обобщения последнего - понятие «животное» (С).

Есть предел обобщения каждого понятия в рамках той или иной науки и безотносительно к той или иной науке. Пределом обобщения является универсальное понятие в рамках науки или безотносительно к той или иной науке.

Символически понятие (А) запишем:

x((S(x) P(x)) R(x, а)), где S, Р, R, а - символы для терминов «млекопитающее», «животное», «обитающее на», «суша». Область значений переменной х - множество тел. Понятие В - x(S(x) P(x)) - получено из А путем отбрасывания одного из признаков. Такой способ обобщения рассматривался в традиционной логике. В современной логике под обобщением понимают переход от некоторого понятия (хА(х)) к другому понятию (хВ(х)), содержание которою меньше содержания первого. Содержание понятия хВ(х) меньше содержания понятия хА(х), если и только если А(х) |- В(х), и неверно, что В(х) |- А(х). Под это определение подпадают и обобщения в традиционном смысле.

Основными способами обобщения понятий являются следующие:

1) понятие формы хВ(х) является результатом обобщения понятия формы х(А(х) В(х)) - традиционный способ обобщения;

2) понятие формы х(А(х) В(х)) является результатом обобщения понятия формы хА(х), например, понятие «число, которое делится на 2 или на 3» является результатом обобщения понятия «число, которое делится на 2»;

3) понятие формы является результатом обобщения понятия формы хА(х, а), например, понятие «человек, желающий изучать какую-либо науку» - результат обобщения понятия «человек, желающий изучать философию»;

4) понятие формы хА(х, а) является результатом обобщения понятия формы , например, понятие «человек, желающий изучать философию» - результат обобщения понятия «человек, желающий изучать все науки».

Возможны, конечно, более сложные способы обобщения понятий, но для всех способов справедливо данное выше определение.

Ограничение понятия - это переход от некоторого понятия к понятию с меньшим объемом, но большим содержанием. Таким образом, ограничение - это операция, обратная операции обобщения. Пределом ограничения является единичное понятие.

Знание формально-логических способов обобщения и ограничения полезно для выяснения отношений между понятиями.

 

 

9.

ГЛАВА VIII. ПРИЕМЫ РАЗЪЯСНЕНИЯ ВЫРАЖЕНИЙ

В научном познании, преподавании и в некоторых других областях человеческой деятельности применяются различные приемы разъяснения языковых выражений. Этими приемами являются определение, а также приемы, называемые приемами, сходными с определением.

9.1.

§ 1. Определение

Понятие определения

Древнегреческий термин, соответствующий русскому слову «определение», происходит от греческого слова «хорос», что означает «пограничный столб». Такие столбы ставились, чтобы отделить один участок земли от другого. Латинское слово «definitio» (определение, или дефиниция) образовано от слова «finis» - «граница», «конец чего-либо», русское слово «определение» - от слов «делить», «устанавливать границу (употребления выражения)».

Определение - это логическая операция, заключающаяся в придании точного смысла языковому выражению, который позволяет, когда то требуется, выделить или уточнить значение этого выражения.

Специфической особенностью науки и рациональной философии является употребление терминов, разъясняемых посредством определений. (В каждой науке используются и неопределяемые термины. Это термины других наук, а также те, которые разъясняются при помощи приемов, сходных с определением.)

Определение решает следующую задачу: выделить систему признаков, общую и отличительную для предметов, обозначаемых термином. В научном познании эта задача часто усиливается требованием найти систему существенных признаков, важных в каком-либо отношении, например для решения тех или иных практических задач.

Логика указывает способы и правила определения, систематизирует типичные ошибки, возникающие при нарушении этих правил. Выделение системы существенных признаков тех или иных предметов - задача конкретных наук. Эта задача сложная. Предпринималось много попыток решить эту задачу относительно человека. Платон, например, определял человека как животное двуногое, но без перьев. Аристотель определял человека как общественное животное. Гельвеций - как животное, обладающее особой внешней организацией, руками и пользующееся орудиями и оружием. Франклин человек - животное, способное производить орудия труда. В «Тезисах о Фейербахе» К. Маркс писал: «...сущность человека не есть абстракт, присущий отдельному индивиду. В своей действительности она есть совокупность всех общественных отношений» . По Марксу, сущность человека следует искать не в индивиде, а в обществе. Проблема выявления сущности человека требует дальнейшего исследования.

Определение, в котором указывается система существенных признаков предметов, является результатом сложного процесса познания.

В научном познании применяются определения различных видов. В учебнике излагаются лишь наиболее часто употребляемые из них.

Прежде всего, различают номинальные и реальные определения.

Номинальные определения - это соглашения или указания относительно смысла вновь вводимых языковых выражений, а также о том, в каком из различных имеющихся смыслов следует употреблять выражение в данном контексте или какой новый смысл, в отличие от принятых смыслов, придается выражению.

Реальными являются определения, в которых придается точный смысл выражениям, значения которых с большей или меньшей степенью определенности уже известны. Посредством реальных определений вводятся понятия о предметах, обозначаемых термином, т.е. решается задача выделения системы признаков, общей и отличительной для этих предметов. Реальные определения иногда называют определениями вещей, а номинальные - определениями названий.

Номинальные определения - это соглашения или указания о том, как будет употребляться термин. Результаты таких определений нельзя оценивать как истинные или ложные. Например, если мы договоримся называть наиболее простые методы познания приемами познания, то указанные оценки к этому соглашению применять нет смысла. На основе реальных определений можно образовать суждения, которые могут быть истинными или ложными . Кроме того, те и другие определения могут быть правильными и неправильными. Это зависит от соблюдения правил, излагаемых в этом параграфе ниже. (Наборы правил для тех и других определений не полностью совпадают.)

Номинальные определения от реальных можно отличить лишь по контекстам, в которых они употребляются, если определения не содержат таких слов, как «будем употреблять то-то выражение в таком-то смысле» и т.д.

Пример номинального определения: «Будем называть гомеостазисом совокупность внешних условий, обеспечивающих возможность существования данного организма».

Определения делятся на номинальные и реальные по той функции, которую они выполняют в познании. Можно также подразделить определения на два вида по форме. Этими видами являются явные и неявные определения.

Явными называются определения, которые имеют структуру: «А есть В» или «А тогда, и только тогда, когда В», где А - определяемое выражение, а В - определяющее. Определяемое выражение называется дефиниендумом (от лат. definiendum, сокращенно: dfd), а определяющее - дефиниенсом (от лат. definiens, сокращенно dfn).

Неявные определения такой формы не имеют.

Видами неявных определений являются определения (а) через отношение к противоположному; (б) контекстуальные; (в) индуктивные; (г) рекурсивные и др.

Явные определения

Определяемыми выражениями в явных определениях могут быть: (1) выражения типа единичных; (2) типа общих имен; (3) предметные функторы; (4) предикаты; (5) предложения.

Если использовать указанные сокращения определяемого и определяющего выражений, то определение можно представить так: . Читается: «dfd есть то же самое, что и dfn», или «dfd тождественно по определению (по дефиниции) dfh». Иногда понимают выражение «» как равенство и при определении предикатов и предложений используют запись . Тогда выражение читается так: dfd эквивалентно по определению (по дефиниции) dfn.

Примеры:

(1) «Онкология - наука об опухолях и их лечении».

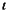Символическая запись: где а - онкология; - оператор определенной дескрипции (выражение читается: тот (единственный) х, который); Р и Q - соответственно предикаторы «изучающая опухоли» и «изучающая лечение опухолей». Область значений х - множество наук.

(2) «Студент - это человек, который учится в высшем гражданском учебном заведении».

Определяющая часть - это выражение т.е. х такой, что существует y такое, что y - высшее учебное заведение (Р) и y - гражданское (Q), и учится (R(x, y)) х в y. Как быть с определяемой частью? При содержательном подходе должно быть. так: где S - общее имя «Студент» . Однако в этом случае нарушается правило возможности взаимной замены определяемой и определяющей частей в текстах. Чтобы такая замена производилась без нарушения смыслов выражений, необходимо соблюдать правило: в определяемой и определяющей частях должны содержаться одни и те же свободные переменные. Есть возможность избежать нарушения этого правила. Для этого при определении (неописательного) общего имени нужно заменить его coответствующим описательным именем. Например, в приведенном примере взять в качестве дефиниендума выражение xS(x), которое означает «человек, который является студентом». Получаем запись определения:

* Вторая возможность. Можно использовать особое исчисление, в котором предикатные символы обозначают неописательные общие имена. Квантификация производится тоже по неописательным общим именам. Например, суждение «Все металлы электропроводны» выражается на этом языке так: 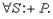Плюсом обозначается связка «суть» («есть»). Суждение «Ни один металл не пластичен» - Знак «-» обозначает связку «не суть» («не есть»). Плюс в формулах опускается. Определение общего имени «студент» на этом языке будет выражено так: 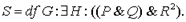Читается: студент есть человек (G) такой, что существует учебное заведение (Н) такое, что оно высшее (Р), гражданское (Q) и этот человек учится () в нем. В первом случае определение выражения S является неявным, контекстуальным. Во втором случае явным.

(3) Вес - то общее, что есть у всех тел, которые притягиваются к Земле с одной и той же силой (уравновешиваются на весах).

Определяющую часть можно представить так: Читается: та функция (F), для которой верно, что для каждого х и для каждого y имеет место, что они притягиваются к Земле с одной и той же силой тогда и только тогда, когда применение этой функции к х есть тот же самый предмет, что и при применении этой функции к y.

Определение:

(4) «Быть студентом - учиться в высшем учебном заведении гражданского типа».

Символическую запись можно получить из определения (2) -

Получаем:

(5) «Петров Павел - студент» означает, что он учится в высшем гражданском учебном заведении».

Символически:

Таким образом, общие формы рассмотренных определений таковы:

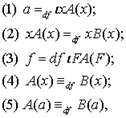
а в более общем виде: где А и В - высказывания. (В еще более общем виде - предложения, выражающие суждения, или вопросы, или нормы).

Наиболее распространенными явными определениями являются определения выражений типа единичных и общих имен, называемые определениями через род и видовое отличие, которые в свою очередь делятся на: а) атрибутивно-реляционные; б) генетические; в) операциональные.

Определения через род и видовое отличие.

Пример. Электростимуляция - лечебный метод, который заключается в применении импульсов электрического тока минимальной силы для поддержания питания и нормального функционирования поврежденного нервно-мышечного аппарата.

В этом определении электростимуляция выделяется среди всех лечебных методов путем указания свойств: «заключаться в применении импульсов электрического тока минимальной силы для поддержания питания и нормального функционирования поврежденного нервно-мышечного аппарата». Множество предметов, в котором выделяются определяемые предметы, называется родом. В данном примере родом является множество лечебных методов. Та система признаков, с помощью которой выделяются определяемые предметы среди других предметов рода, носит название видового отличия.

В атрибутивно-реляционных определениях видовым отличием являются качества (атрибуты) и отношения (реляции). Качества - это то, что присуще предметам самим по себе, а отношения - это проявление качеств во взаимодействии предметов с другими предметами. Наличие свободных электронов у металлов - это их качество. Проводимость электричества - это отношение, представляющее собой проявление указанного качества во взаимодействии с электрическим полем.

Примеры.

«Человек - это разумное животное» - атрибутивное определение».

«Человек - это животное, которое может заниматься скупкой и перепродажей товаров или иных предметов с целью получения прибыли» - реляционное определение.

В генетических определениях в качестве видового отличия выступает способ происхождения, образования, конструирования предметов. Томас Гоббс приводит следующий пример генетического определения: «Круг есть фигура, получающаяся в результате вращения отрезка прямой вокруг одного из его концов в плоскости» .

Генетические определения достаточны лишь при определении простых объектов, например объектов геометрии. При определении сложных социальных явлений нужно, конечно, показывать, как они возникли, но нужно также указать их качества и (или) отношения к другим явлениям. Можно дополнить генетическое определение атрибутивным (реляционным) или в одном определении указать, как явление возникло и какими свойствами оно характеризуется.

Операциональными являются определения, в которых предметы выделяются посредством указания операций, с помощью которых эти предметы можно распознать или выявить.

Пример: кислота - это жидкость, при погружении в которую лакмусовой бумажки последняя окрашивается в красный цвет. Операция распознавания выполняет здесь роль видового отличия.

Другой вид операциональных определений - выделение предметов путем указания способа их выявления.

Пример: определение логической формы мысли. (Логическая форма мысли - это ее структура, выявляемая в результате частичного отвлечения от смыслов и значений нелогических терминов, входящих в словосочетание, выражающее эту мысль.)

При характеристике абстрактных понятий дано описание определений через абстракцию. Абстрактные понятия - это понятия о предметных функциях. Выделены два вида абстрактных понятий: понятия единичные («краснота») и общие («вес»). Рассмотрим пример определения понятия целого положительного числа (далее - числа). Разбиваем множества предметов на классы. В каждый класс включаются множества, между элементами которых можно установить одно-однозначное отношение. Число - то общее, что есть у всех множеств, находящихся в таком отношении. Это понятие числа абстрактное. Назовем его первичным понятием числа. Далее, применяя функцию, выражаемую этим понятием к множествам, будем получать значения. Например, применяя эту функцию, обозначим ее знаком Ф, к множеству , получим объект Ф(). Обозначим его знаком 1. Далее, Ф() пусть есть 2. И так далее. Образуем новое понятие числа. Это общее конкретное понятие.

Неявные определения

1. Определения через отношение к противоположному. Эти определения применяются, например, в философии. В них определяются сразу два термина путем указания отношения предметов, обозначаемых одним из этих терминов, к предметам, обозначаемым другим из этих терминов. Пример: причина - это явление, которое при определенных условиях обязательно вызывает другое явление, называемое следствием.

2. Контекстуальные определения. В контекстуальных определениях выясняется смысл контекста, в который входит определяемый термин. Например, Контекстуальное определении имеет форму 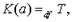если К(а) - сложное имя, а а - имя, входящее в К(а).

Контекстуальные определения указанных форм называются нормальными.

Существуют контекстуальные определения, которые не имеют вида и

Пример. Определение выражения «возможно» (М).

 

	М А
1.	? и
2.	л л

«?» означает «то ли истинно, то ли ложно». Рассмотрим обе возможности:

 

	М А
1'.	и и
1''.	л и
2.	л л

Иначе:

Применяется еще один вид контекстуальных определений - определения в контексте. В качестве определения здесь выступает контекст, представляющий собой текст, состоящий из ряда высказываний, в которых употребляется определяемый термин. В самом контексте, как и вне контекста, не говорится, что имеет место определение термина. Если же контекст внимательно проанализировать, то из него можно «вычитать» определение указанного термина. Например, исследуя свидетельства древних авторов о философских взглядах Демокрита, выявляют определение причины в смысле Демокрита. Средствами символической логики удалось показать, что не всякий контекст, в котором встречается термин, является определением (в контексте) этого термина. Так из слов песни: «Живет моя отрада в высоком терему, и в терем тот высокий нет хода никому» нельзя выделить определение слова «отрада».