Глава 30. Треугольники. С

№30.18) В треугольнике АВС точка Н является точкой пересечения высот. Известно, что АВ=СН. Найдите угол АСВ.

№30.19) В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длины 2 и 5. Найти площадь треугольника.

№30.19.1) Найдите стороны треугольника 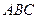, если биссектриса угла и медиана, проведенная из вершины 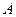, взаимно перпендикулярны и имеют одинаковую длину, равную 28.

Ответы к главе 32. №30.18) ; №30.19) 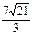; №30.19.1) .

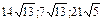Глава 31. Четырехугольники (трапеция, параллелограмм, ромб). С.

№31.11) У трапеции ABCD основание AD в 4 раза больше основания BC, а площадь трапеции равна 50. Точка O – точка пересечения диагоналей, точка P – середина основания AD, точка M – точка пересечения диагонали AC и отрезка BP, точка N – точка пересечения диагонали BD и отрезка CP. Найти площадь треугольника MON.

№31.12) В трапеции ABCD основания BC=2 см, AD=9 см. Точки K и L лежат на боковых сторонах AB и CD так, что отрезок KL параллелен основаниям и делит высоту трапеции в отношении 2:5, считая от меньшего основания. Найти площадь трапеции AKLD, если площадь треугольника ACD равна 63 .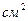

№31.13) В трапеции ABCD основания BC=3 см, AD=10 см. Отрезок KL, концы которого лежат на боковых сторонах AB и CD, параллелен основаниям, и BK:KA=3:4. Найти площадь трапеции AKLD, если площадь трапеции ABCD равна 45,5 .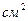

Ответы к главе 31. №31.11) 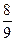; №31.12) 65 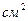; №31.13) 32.