№35.9) Дан куб с основанием 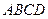 и боковыми ребрами
и боковыми ребрами 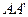 ,
, 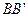 ,
, 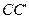 ,
, 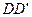 . Длина всех ребер куба равна
. Длина всех ребер куба равна 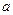 . Через точки
. Через точки 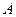 ,
, 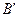 ,
, 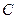 проведена плоскость. Найти расстояние от вершины D’ до этой плоскости.
проведена плоскость. Найти расстояние от вершины D’ до этой плоскости.
№35.10) В тетраэдр, у которого все рёбра равны, вписан конус, а в этот конус вписан шар. Найдите отношение объёма конуса к объёму шара.
№35.11) В правильной треугольной призме 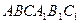 с боковыми ребрами
с боковыми ребрами 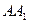 ,
, 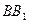 ,
, 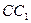 точки M и K – середины отрезков
точки M и K – середины отрезков 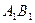 и
и 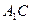 соответственно. Известно, что прямая MK образует угол в
соответственно. Известно, что прямая MK образует угол в 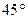 с плоскостью
с плоскостью 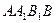 , MK=3. Найти объем призмы
, MK=3. Найти объем призмы 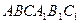 .
.
№35.12) Ребро основания 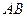 правильной треугольной призмы
правильной треугольной призмы 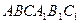 равно 10, боковое ребро
равно 10, боковое ребро 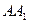 равно 30. На боковом ребре
равно 30. На боковом ребре 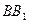 взята точка
взята точка 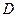 так, что
так, что 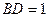 , а на боковом ребре
, а на боковом ребре 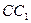 взята точка
взята точка 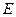 так, что
так, что 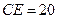 . Найдите расстояние между прямыми
. Найдите расстояние между прямыми 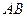 и
и 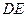 .
.
№35.13) Ребро основания 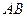 правильной треугольной призмы
правильной треугольной призмы 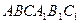 равно 10, боковое ребро
равно 10, боковое ребро 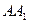 равно 30. На боковом ребре
равно 30. На боковом ребре 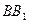 взята точка
взята точка 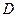 так, что
так, что 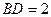 , а на боковом ребре
, а на боковом ребре 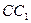 взята точка
взята точка 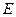 так, что
так, что 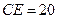 . Найдите расстояние между прямыми
. Найдите расстояние между прямыми 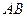 и
и 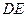 . (Примечание: в других вариантах билетов были те же условия, где менялась
. (Примечание: в других вариантах билетов были те же условия, где менялась 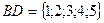 )
)
Ответы к главе 35. №35.9) 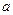 ; №35.10) 2; №35.11) 36; №35.12)
; №35.10) 2; №35.11) 36; №35.12) 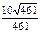 ; №35.13)
; №35.13) 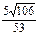 .
.
|
|
|
Глава 37. Параметры. Линейные методы. C. Замена переменной.
№37.23) Определить все действительные значения параметра 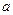 , при каждом из которых уравнение
, при каждом из которых уравнение 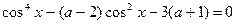 имеет решения и найти все эти решения.
имеет решения и найти все эти решения.
№37.24) Определить все действительные значения параметра 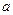 , при каждом из которых уравнение
, при каждом из которых уравнение 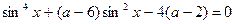 имеет решения и найти все эти решения.
имеет решения и найти все эти решения.
Ответы к главе 37. №37.23) 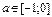 ,
, 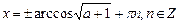 ; №37.24)
; №37.24) 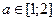 ,
, 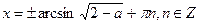 ;
;
 2017-11-01
2017-11-01 303
303







