2017-11-01
504
Уравнение вида
 ,
| (1.106) |
где 
- параметр, учитывающий физические свойства изучаемой среды, называется уравнением теплопроводности.
Оно имеет вид для плоского случая
 ,
| (1.107) |
для одномерного
 .
| (1.108) |
Уравнением теплопроводности описываются процессы нестационарного массо- и теплообмена. В частности, к этим уравнениям приводят задачи о неустановившемся режиме распространения тепла (при этом 
означает коэффициент температуропроводности, а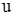 
- температуру в любой точке исследуемой области в любой момент времени 
); о фильтрации упругой жидкости в упругой пористой среде, например, фильтрация нефти и газа в подземных песчаниках (
- коэффициент пьезопроводности, 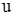- давление в любой точке среды); о неустановившейся диффузии (
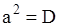- коэффициент диффузии, 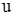- концентрация); о течении жидкости в магистральных трубопроводах ( 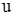- давление или скорость жидкости).
Если при рассмотрении этих задач окажется, что в исследуемой области функционируют внутренние источники и стоки массы или тепла, то процесс описывается неоднородным уравнением
|
|
|
 ,
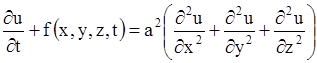| (1.109) |
где функция 
характеризует интенсивность функционирующих источников.
Уравнения (1.106)…(1.109) являются простейшими уравнениями параболического типа.
