Основные определения и понятия

ВВЕДЕНИЕ В ТЕОРИЮ УРАВНЕНИЙ

МАТЕМАТИЧЕСКОЙ ФИЗИКИ

Многие задачи механики и физики могут быть сведены к дифференциальным уравнениям в частных производных. Математическими моделями реальных процессов являются краевые задачи для дифференциальных уравнений при определенных граничных и начальных условиях. При этом оказывается, что одно и то же уравнение может описывать совершенно различные по своей природе явления и процессы. Поэтому при исследовании довольно широкого круга задач механики и физики требуется сравнительно небольшое число различных видов дифференциальных уравнений. Изучением таких уравнений, методами их решения занимается раздел математики «Уравнения математической физики».

В нашем курсе мы будем заниматься уравнениями второго порядка. С помощью этих уравнений можно исследовать в первом приближении основные физические процессы: колебания, теплопроводность, диффузию, течение жидкостей и газа, электростатические явления.

Для решения своих проблем теория «Уравнений математической физики» использует различный математический аппарат: ряды Фурье, интегралы Фурье, интегральные преобразования (Лапласа, Фурье), функции комплексного переменного и др.

Специфическим для уравнений математической физики является то, что здесь постановка задач для уравнений в частных производных делается исходя из физических соображений. Процесс получения решения этих задач основывается на математических методах, но в каждом конкретном случае само решение той или иной задачи должно иметь определенную физическую интерпретацию.

 

 

Дифференциальные уравнения в частных производных.

Основные определения и понятия

Определение 1.40 Уравнение, связывающее неизвестную функцию нескольких переменных и ее частные производные, называется дифференциальным уравнением в частных производных.

Порядок высшей частной производной, входящей в уравнение, определяет порядок уравнения.

Для функции 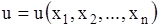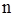независимых переменных 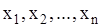уравнение 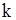-го порядка имеет вид

 

.

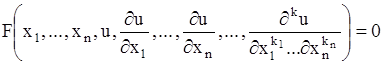(1.79)

 

.

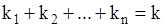Обычно приходится иметь дело с уравнениями для функций двух, трех, четырех переменных.

Общий вид уравнений первого и второго порядков для функции 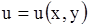двух переменных соответственно таков:

 

,

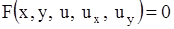(1.80)

 

,

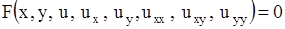(1.81)

 

где

, , , , .

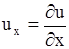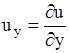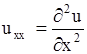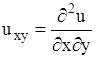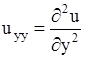Решением уравнения в частных производных (1.79) называется всякая функция 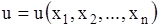( 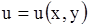для уравнений (1.80), (1.81)), которая, будучи подставлена в уравнение вместо неизвестной функции и ее частных производных, обращает это уравнение в тождество по независимым переменным.