Линейные уравнения второго порядка в частных производных делят на три класса, в каждом из которых есть простейшие уравнения, называемые каноническими. Решения уравнений одного и того же класса имеют много общих свойств. Для изучения этих свойств достаточно рассмотреть канонические уравнения, так как другие уравнения данного типа могут быть приведены к каноническому виду.
Запишем линейное относительно производных второго порядка уравнение (1.88) в более краткой форме:
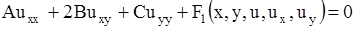 . .
| (1.92) |
Классификация уравнений вида (1.92) проводится в соответствии со знаком дискриминанта 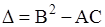 .
.
Если в некоторой области 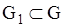 выражение
выражение 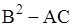 сохраняет знак, то уравнение (1.92) в этой области принадлежит:
сохраняет знак, то уравнение (1.92) в этой области принадлежит:
а) к гиперболическому типу, если 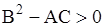 ;
;
б) параболическому типу, если 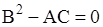 ;
;
в) эллиптическому типу, если 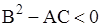 .
.
Пример. Определить тип уравнения
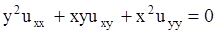 .
.
Решение. Здесь 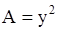 ,
, 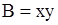 ,
, 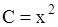 и
и 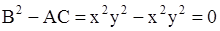 для любых
для любых 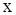 и
и 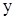 . Значит, на всей плоскости, а следовательно и в некоторой области задания, данное уравнение является уравнением параболического типа.
. Значит, на всей плоскости, а следовательно и в некоторой области задания, данное уравнение является уравнением параболического типа.
Если уравнение рассматривается в области задания 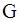 , то указанные три типа не всегда дают исчерпывающую классификацию, так как выражение
, то указанные три типа не всегда дают исчерпывающую классификацию, так как выражение 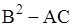 может не сохранять знак во всей области. Тогда должна существовать кривая
может не сохранять знак во всей области. Тогда должна существовать кривая 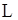 , вдоль которой выражение
, вдоль которой выражение 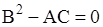 ; эта кривая называется линией параболического вырождения. При этом возможны два случая:
; эта кривая называется линией параболического вырождения. При этом возможны два случая:
1) во всех точках 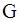 , кроме
, кроме 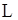 ,
, 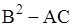 сохраняет знак, тогда уравнение (1.92) называется уравнением гиперболического или эллиптического типа с линией вырождения
сохраняет знак, тогда уравнение (1.92) называется уравнением гиперболического или эллиптического типа с линией вырождения 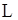 ;
;
2) выражение 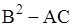 меняет знак в области
меняет знак в области 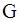 , тогда уравнение (1.92) называется уравнением смешанного типа.
, тогда уравнение (1.92) называется уравнением смешанного типа.
Пример. Определить тип уравнения
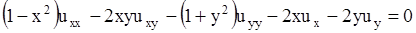 .
.
Решение. Здесь 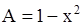 ,
, 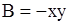 ,
, 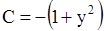 и, следовательно,
и, следовательно, 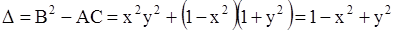 . Дискриминант
. Дискриминант 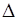 равен нулю, когда
равен нулю, когда 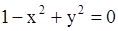 . Значит, гипербола
. Значит, гипербола 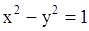 является линией параболического вырождения, а данное уравнение относится к смешанному типу, причем области
является линией параболического вырождения, а данное уравнение относится к смешанному типу, причем области 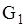 , где
, где 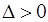
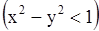 , и
, и 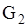 , где
, где 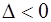
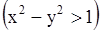 , являются областями гиперболичности и эллиптичности.
, являются областями гиперболичности и эллиптичности.
Уравнение вида
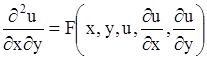
| (1.93) |
называется каноническим уравнением гиперболического типа.
Второй канонический вид уравнения гиперболического типа таков:
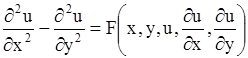 . .
| (1.94) |
Уравнение вида
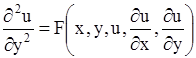
| (1.95) |
называется каноническим уравнением параболического типа.
Уравнение вида
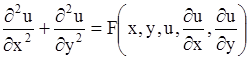
| (1.96) |
называется каноническим уравнением эллиптического типа.
 2017-11-01
2017-11-01 350
350








