Аппрокисмация функции по Фурье

Пусть функция задана в интервале . В этом случае (при наличии у нее соответствующих свойств интегрируемости) можно построить ряд Фурье этой функции, а именно объект

где

Известно, что для непрерывной функции этот ряд сходится в каждой точке интервала и притом - к значению в этой точке функции . Если суммирование в ряду Фурье прервать на каком-то слагаемом, то возникнет приближенное равенство

которое тем точнее, чем больше число слагаемых в сумме. В этом и состоит аппроксимация функции по Фурье.

Практически организация расчетов при аппроксимации происходит так: задается та степень точности e, с которой надо приблизить число с помощью частичных сумм ряда (7.1.1); затем вычисляют, постепенно наращивая количество слагаемых, частичные суммы ряда (7.1.1) и делают это до тех пор, пока два раза подряд не получится при суммировании одно и то же с точностью e число; его и принимают за нужное приближение. Естественно, что при вычислении частичных сумм ряда требуются коэффициенты , которые вычисляются с помощью численного интегрирования через определяющие равенства.

Описанная ситуация обобщается на случай функции , заданной не на интервале , а на произвольном интервале . В этом случае (для непрерывной функции ) имеет место равенство

внутри интервала ,

где

Принято выделять случаи четной и нечетной функции, так как при этом вычисление коэффициентов существенно упрощается, а именно:

если на интервале функция четная, то для всех имеют место равенства и

;

если на интервале функция нечетная, то для всех имеют место равенства и

Это обстоятельство подсказывает выход из положения, при котором функция задана не на интервале , а только на интервале : функцию можно продолжить на весь интервал четным или нечетным образом, а затем произвести разложение Фурье.

Конструкция Фурье может рассматриваться и на любом интервале благодаря периодичности функций , так что равенство можно рассматривать на всей числовой прямой, кроме, возможно, точек .

5.2 Преобразование Фурье

Преобоазование Фурье - действие, с помощью которого по заданной в интервале функции строится система чисел. По традиции, именно эти числа также обозначают словами «преобразование Фурье» данной функции. При этом числа называются косинус-преобразованием Фурье функции , а числа называются синус-преобразованием Фурье функции . У преобразования Фурье функции есть множество свойств и применений; в частности,

известен ряд прикладных вопросов, в которых ту или иную информацию о функции удается получить только через ее преобразование Фурье, которое в таких ситуациях удается получить некоторыми косвенными средствами.

Рассмотрим следующий частный случай. Функция рассматривается не на интервале (-p,p), а на интервале (0,2π) и притом только в его отдельных точках

при некотором заранее заданном и фиксированном числе . Значения функции в этих точках считаются известными; обозначим

В равенстве

положим . Получим

Проанализируем данное соотношение. Если произвольное целое неотрицательное число разделить с остатком на число , то получится соотношение , где для целых имеются лишь следующие возможности: .

С учетом периодичности косинуса и синуса в выражении можно привести подобные члены, в результате чего получится:

где

Отметим, что теперь все суммы конечны. Известен следующий факт о тригонометрических суммах:

для всех чисел имеют место равенства

Если обе части соотношения умножить на и затем просуммировать по , то, с учетом только что сказанного, легко получить, что

;

а если обе части умножить на и, с учетом того же утверждения о суммировании косинусов и синусов, получим соотношение

причем .

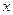Числа , называются дискретным преобразованием Фурье функции . Если заменить на произвольный , то оно из точного станет приближенным. Его правую часть в этом случае называют тригонометрической интерполяцией функции .

5.3 Быстрое преобразование Фурье

В предыдущем пункте было описано дискретное преобразование Фурье - сопоставление набору значений функции набора коэффициентов . Процесс этого сопоставления в некоторых случаях можно ускорить, специальным образом организовав соответствующие суммирования.

Предположим, что число является составным,т.е. при натуральных . Разделим с остатком число на и число (индекс суммирования) на ; получим: .

Заметим, что в образовавшихся обозначениях суммирование по эквивалентное повторному суммированию по схеме:

;

преобразуем теперь суммируемое выражение:

введем обозначения:

;

тогда выражение представляется в виде:

Совершенно аналогично можно провести рассуждения с коэффициентом , в результате чего снова возникнут те же ; в итоге получится:

отсюда возникает соотношение:

Отсюда возникает иная возможность вычисления дискретного преобразования Фурье, отличная от прямого вычисления: надо сначала найти выражения , а затем уже сами числа ; потребуется, как нетрудно заметить, меньше арифметических операций. Отсюда и название - «Быстрое преобразование Фурье»