Алгоритм 1.2 (Алгоритм метода дихотомии)

Шаг 1. Ввести исходные данные: a, b, d, e.

Шаг 2. Определить x1 и x2 по формулам (1.5).

Шаг 3. Вычислить f(x1) и f(x2).

Шаг 4. Если f(x1) £ f(x2), то перейти к новому отрезку [a, b], положив b = x2. Иначе перейти к новому отрезку [a, b], положив a = x1.

Шаг 5. Если 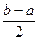< e, то требуемая точность достигнута, перейти к шагу 6, иначе – к шагу 2 для продолжения итераций.

Шаг 6. Положить x*» 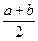. Вычислить f *» f(x*).

Число итераций метода дихотомии оценивается по формуле

n ³ log2 .

Величину d выбирают из условия 0 < d < 2e. При этом нужно иметь в виду, что при слишком малом d из-за погрешности вычисления на ЭВМ сравнение f(x1) и f(x2) становится затруднительным.

Реализация данной задачи в пакете MathCAD 14

Данную задачу решаем для следующей функции:

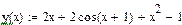
Задание функции, реализующей метод деления отрезка пополам с заданной точностью:

В результате решения данной задачи был найден минимум x* =-1, значение функции f(x*) = 0, количество итераций n = 11.

Метод Фибоначчи

Найти минимум функции методом Фибоначчи с заданной точностью.

Метод Фибоначчи эффективнее метода дихотомии, так как разбиение отрезка производится таким образом, что на каждой итерации требуется вычислять не два значения f(x1) и f(x2), а лишь одно.

Метод Фибоначчи основан на использовании чисел Фибоначчи, задаваемых рекуррентным соотношением

Fn = Fn-1 + Fn-2 (n ³ 2)

с начальными значениями F0 = 1, F1 = 1.

Этот метод был предложен в 1953 г. Кифером.

Формула вместе с начальными значениями определяет следующий ряд чисел Фибоначчи:

n	0 1 2 3 4 5 6 7 8 9 10 11 …
Fn	1 1 2 3 5 8 13 21 34 55 89 144 …

Метод Фибоначчи состоит из n шагов.

Положим вначале a0 = a, b0 = b.

На k-ом шаге, k =0, 1, …, n – 1, определим точки x и x из условия

x = ak + (bk – ak), x = ak + (bk – ak).

Формулы являются основными расчетными формулами метода Фибоначчи

После этого так же, как и в методе дихотомии, определяют новый, меньший отрезок локализации [ak+1, bk+1] по тому же правилу:

если f(x ) £ f(x ), то ak+1 = ak, bk+1 = x ;

если f(x ) > f(x ), то ak+1 = x , bk+1 = bk.

Важно, что одна из пробных точек x , x станет пробной точкой на новом отрезке локализации, т. е. совпадет с одной из точек x , x .

Поэтому на каждой итерации достаточно определить только одно значение f(x), так как другое уже найдено на предыдущей итерации.

В конце вычислений можно взять в качестве приближенного значения

экстремум минимизация функция линейный

x* = x .

После выполнения n итераций погрешность удовлетворяет следующему неравенству:

en = < .

Следовательно, если задана требуемая точность e, число итераций n определяется из условия < e или

Fn +1 > .

Заметим, что число итераций, необходимое для удовлетворения заданной точности e, зависит только от длины отрезка b – a и точности e и не зависит от вида функции f(x).

Алгоритм 1.3 (Алгоритм метода Фибоначчи):

Шаг 1. Ввести исходные данные: a, b, e. Определить число итераций n из условия (1.9). Ввести числа Фибоначчи F0, F1, F2, …, Fn +1.

Шаг 2. Положить k = 0 и определить x1 и x2 по формулам (1.7).

Шаг 3. Вычислить f(x1) и f(x2).

Шаг 4. Проверить критерий окончания вычислений: k = n. Если k < n, перейти к шагу 5, иначе – к шагу 6.

Шаг 5. Перейти к новому отрезку локализации и новым пробным точкам. Если f(x1) £ f(x2), то положить b = x2, x2 = x1, f(x2) = f(x1), x1= a + (b – a) и вычислить f(x1). Иначе положить a = x1, x1 = x2, f(x1) = f(x2),

x2 = a + (b – a) и вычислить f(x2). Положить k = k +1 и перейти к шагу 4.

Шаг 6. Положить x*» x1. Вычислить f *» f(x*).

Данную задачу мы решаем для следующей функции:

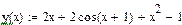
Задание функции, реализующей метод Фибоначчи с заданной точностью:

В результате решения данной задачи был найден минимум x* = -1, значение функции f(x*) = 5.329*10^-15, количество итераций n = 8.

Метод золотого сечения

Найти минимум функции методом золотого сечения с заданной точностью.

В основе этого метода лежит понятие "золотого сечения", введенного Леонардо да Винчи и используемого, в частности, при построении архитектурных сооружений античности и эпохи Возрождения.

Золотым сечением отрезка называется его разбиение на две неравные части, так, что отношение длины всего отрезка к длине его большей части равно отношению длины большей части к длине меньшей части (рис.1.3, слева)

= .

Рис 1.3

Золотое сечение осуществляется двумя точками x1 и x2, расположенными симметрично относительно середины отрезка (рис.1.3, справа). Нетрудно проверить, что

= = , (1.10)

= = . (1.11)

Точка x1 осуществляет золотое сечение не только отрезка [a, b], но и отрезка [a, x2], а точка x2 осуществляет золотое сечение не только отрезка [a, b], но и отрезка [x1, b]. Действительно,

= = ,

= = .

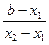Из (1.10) и (1.11) получаем:

x1 = a + , x2 = a + . (1.12)

Формулы (1.12) являются основными расчетными формулами метода золотого сечения.

Из (1.12) следует, что x1 + x2 = a + b. Если обозначить r = 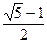, то формулы (1.12) можно переписать так:

x1 = b – r(b – a), x2 = a + r(b – a) (1.13)

Процедура деления отрезка [a, b] такая же, как и для методов дихотомии и Фибоначчи. Вычисляются значения функции в выбранных точках: f(x1) и f(x2). Определяется новый отрезок локализации [a1, b1] следующим образом:

если f(x1) £ f(x2), то a1 = a, b1 = x2;

если f(x1) > f(x2), то a1 = x1, b1 = b.

Далее процедура деления отрезка [a1, b1] повторяется с использованием формул (1.12) или (1.13).

Так же, как и в методе Фибоначчи, одна из пробных точек x1, x2 станет пробной точкой на новом отрезке локализации. Поэтому на каждой итерации достаточно определить только одно значение f(x), так как другое уже найдено на предыдущей итерации.

В конце вычислений можно взять в качестве приближенного значения x* середину последнего из полученных отрезков.

После выполнения n итераций погрешность удовлетворяет следующему неравенству:

en = < .