Алгоритм 1.4 (Алгоритм метода золотого сечения)

Шаг 1. Ввести исходные данные: a, b, e. Положить r = 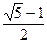, en = .

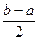Шаг 2. Определить x1 и x2 по формулам (1.13).

Шаг 3. Вычислить f(x1) и f(x2).

Шаг 4. Проверить критерий окончания вычислений. Если en <e, перейти к шагу 5, иначе – к шагу 6.

Шаг 5. Перейти к новому отрезку локализации и новым пробным точкам. Если f(x1) £ f(x2), то положить b = x2, x2 = x1, f(x2) = f(x1), x1 = b – r(b – a) и вычислить f(x1). Иначе положить a = x1, x1 = x2, f(x1) = f(x2), x2 = a + r(b – a) и вычислить f(x2). Положить en = ren, перейти к шагу 4.

Шаг 6. Положить x*» 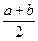. Вычислить f *» f(x*).

Реализация данной задачи в пакете MathCAD 14

Данную задачу мы решаем для следующей функции:

 

 

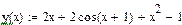
Задание функции, реализующей метод золотого сечения с заданной точностью:

 

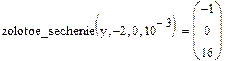
В результате решения данной задачи был найден минимум x* = -1, значение функции f(x*) = 0, количество итераций n = 16.

 

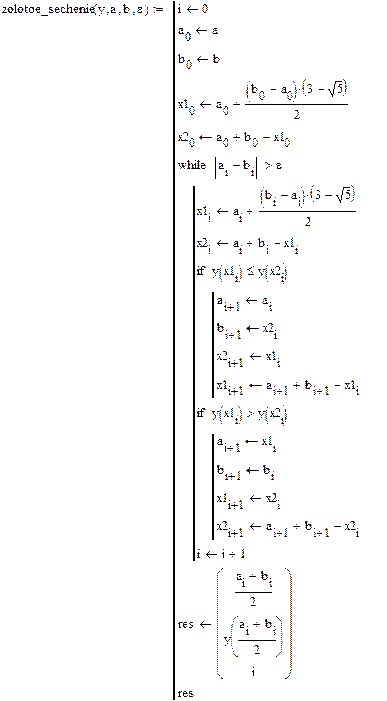
Метод средней точки

Найти минимум функции методом средней точки с заданной точностью.

Все методы, рассмотренные до сих пор, основаны на предположении об унимодальности исследуемой функции. Эти методы используют вычисление значений функции в некоторых точках и не требуют вычисления значений производной функции. Использование информации о производной позволит повысить эффективность решения задачи оптимизации.

Рассмотрим метод средней точки, который называется также методом бисекции или методом деления отрезка пополам.

Пусть f(x) – унимодальная, непрерывно дифференцируемая на отрезке [a, b] функция и на этом отрезке точка x* является единственной стационарной точкой. Сведем задачу нахождения минимума функции f(x) к решению нелинейного уравнения

 

f '(x) = 0. (1.14)

 

Положим a0 = a, b0 = b.

Так как функция f '(x) удовлетворяет условию (1.14), то она принимает на концах отрезка [a0, b0] значения разных знаков, т.е. f(a0)f(b0) < 0.

Разделим отрезок [a0, b0] пополам. Получим точку x0 = 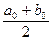. Вычислим f '(x0). Если f '(x0) = 0, то x0 – искомый корень, и задача решена. Если f '(x0) ¹ 0, то f '(x0) – число определенного знака: f '(x0) > 0, либо f '(x0) < 0. Тогда либо на концах отрезка [a0, x0], либо на концах отрезка [x0, b0] значения функции f '(x) имеют разные знаки. Обозначим такой отрезок [a1, b1]. Очевидно, что x*Î [a1, b1], и длина отрезка [a1, b1] в два раза меньше, чем длина отрезка [a0, b0]. Поступим аналогично с отрезком [a1, b1]. В результате получим либо корень x*, либо новый отрезок [a2, b2], и т.д. (рис.1.4).

 

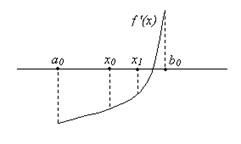
Рис. 1.4

Середина n-го отрезка xn = 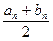. Очевидно, что длина отрезка [an, bn] будет равна 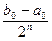, а т. к. x*Î [an, bn], то

| xn – x*| £ 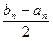£ 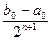. (1.15)

 

Оценка (1.15) характеризует погрешность метода средней точки и указывает на скорость сходимости: метод сходится со скоростью геометрической прогрессии, знаменатель которой q = 1/2.

Если задана требуемая точность e, то процесс вычислений следует закончить, когда выполнится условие ê f '(xn) ê£ e, после чего полагают

x*» xn.