Расходящийся ряд, таким образом, либо имеет бесконечную сумму, либо вовсе не имеет суммы

Рассмотрим примеры.

Пример 1. Показать, что ряд сходится, и найти его сумму.

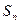Решение. Чтобы воспользоваться формулой (5), следует представить -ю частичную сумму в компактной форме. С этой целью преобразуем общий член ряда к виду:

,

после чего для -ой частичной суммы получаем

.

Нетрудно видеть, что все члены в скобках, за исключением трех первых положительных и трех последних отрицательных, взаимно уничтожаются, так что выражение для -ой частичной суммы 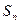принимает вид

,

используя его в (5), находим

,

откуда следует, что рассматриваемый ряд сходится и имеет сумму .

Пример 2. Исследовать сходимость арифметической прогрессии .

Решение. Найдем -ю частичную сумму ряда:

,

то есть

Используя ее в (5), получаем

.

Так как предел бесконечен и не зависит ни от первого члена прогрессии , ни от разности , то отсюда следует, что арифметическая прогрессия всегда расходится.

Пример 3. Исследовать сходимость ряда .

Решение. Выпишем частичные суммы четного и нечетного числа членов ряда:

,

.

Так как , а , то предел последовательности частичных сумм ряда не существует, то есть ряд суммы не имеет и, следовательно, расходится.

5.

1.2 Геометрическая прогрессия