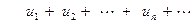 .
.
Его сумма
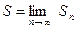
и при достаточно больших 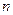 можно приближенно полагать
можно приближенно полагать
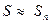 ,
,
причем точность такой замены будет повышаться с ростом 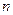 . Для оценки точности введем понятие остатка ряда.
. Для оценки точности введем понятие остатка ряда.
Определение. Разность между суммой ряда 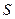 и его
и его 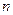 -ой частичной суммой называется n -ым остатком ряда:
-ой частичной суммой называется n -ым остатком ряда:
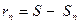 .
.
Очевидно, для сходящегося ряда
 .
.
Для оценки остатка ряда существуют следующие теоремы (которые мы приводим без доказательства)
Теорема 1. (об оценке остатка знакоположительного ряда) Если все члены сходящегося знакоположительного ряда
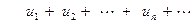
не превосходят соответствующих членов другого сходящегося знакоположительного ряда
 ,
,
то 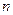 -й остаток первого ряда не превосходит
-й остаток первого ряда не превосходит 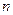 -го остатка второго ряда.
-го остатка второго ряда.
Теорема 2. (об оценке остатка знакопеременного ряда) Пусть знакопеременный ряд
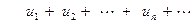
абсолютно сходится. Тогда его  -й остаток по абсолютной величине не превосходит
-й остаток по абсолютной величине не превосходит 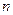 -го остатка ряда, составленного из абсолютных величин его членов.
-го остатка ряда, составленного из абсолютных величин его членов.
Теорема 3. (об оценке остатка знакочередующегося ряда) Абсолютная величина  -го остатка знакочередующегося ряда, сходящегося по признаку Лейбница, не превышает модуля первого из отброшенных членов, т. е.
-го остатка знакочередующегося ряда, сходящегося по признаку Лейбница, не превышает модуля первого из отброшенных членов, т. е. 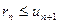 .
.
Пример 15. Вычислить сумму ряда  с погрешностью не более 0.001
с погрешностью не более 0.001
Решение. Выпишем несколько первых членов ряда
 .
.
Так как это знакочередующийся ряд, то погрешность, возникающая при обрывании ряда, не превышает абсолютной величины первого из отбрасываемых членов. Проводя оценки
 ,
,  ,
,  ,
,
видим, что для достижения требуемой точности достаточно учесть пять первых членов. Таким образом, с погрешностью не более 0.001:
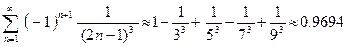 .
.
Лекция 4.
Функциональные ряды
4.1 Понятие функционального ряда. Область сходимости
Определение 1. Ряд, вида
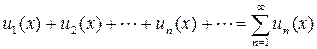 , (1)
, (1)
члены которого являются функциями переменного  , называется функциональным рядом.
, называется функциональным рядом.
Если ряд (1) сходится при некотором  , то точка
, то точка  называется точкой сходимости ряда. Множество всех точек сходимости ряда образует область сходимости ряда. В общем случае область сходимости может быть весьма сложной и состоять из совокупности интервалов. Определение области сходимости можно проводить применяя какой либо признак сходимости знакоположительных рядов, например, признак Даламбера или радикальный признак Коши к ряду, составленному из абсолютных величин членов ряда (1). В интервалах сходимости функциональный ряд (1) сходится абсолютно. Чтобы исследовать сходимость на концах интервалов сходимости, следует подставить в ряд вместо
называется точкой сходимости ряда. Множество всех точек сходимости ряда образует область сходимости ряда. В общем случае область сходимости может быть весьма сложной и состоять из совокупности интервалов. Определение области сходимости можно проводить применяя какой либо признак сходимости знакоположительных рядов, например, признак Даламбера или радикальный признак Коши к ряду, составленному из абсолютных величин членов ряда (1). В интервалах сходимости функциональный ряд (1) сходится абсолютно. Чтобы исследовать сходимость на концах интервалов сходимости, следует подставить в ряд вместо  значения концевых точек интервалов и исследовать сходимость получившихся числовых рядов.
значения концевых точек интервалов и исследовать сходимость получившихся числовых рядов.
Пример 1. Найти область сходимости ряда 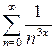 .
.
Решение. При любом фиксированном  получаем обобщенный гармонический ряд вида
получаем обобщенный гармонический ряд вида  . Этот ряд сходится, если
. Этот ряд сходится, если  . То есть, областью сходимости ряда является интервал
. То есть, областью сходимости ряда является интервал 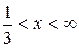 . В точке
. В точке  ряд принимает вид:
ряд принимает вид:  . Это расходящийся гармонический ряд. Итак, окончательно, областью сходимости заданного ряда служит интервал
. Это расходящийся гармонический ряд. Итак, окончательно, областью сходимости заданного ряда служит интервал 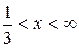 .
.
Пример 2. Исследовать сходимость ряда  .
.
Решение. Прежде всего, заметим, что ряд расходится, если 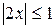 , так как в этом случае
, так как в этом случае 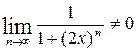 , то есть не выполняется необходимый признак сходимости. Пусть
, то есть не выполняется необходимый признак сходимости. Пусть  . Применяя признак Даламбера к ряду, составленному из абсолютных величин членов данного ряда, находим, что этот ряд сходится, если
. Применяя признак Даламбера к ряду, составленному из абсолютных величин членов данного ряда, находим, что этот ряд сходится, если

то есть при  . Таким образом, ряд абсолютно сходится в интервалах
. Таким образом, ряд абсолютно сходится в интервалах  и
и  , и расходится вне этих интервалов.
, и расходится вне этих интервалов.
4.2 Равномерная (правильная) сходимость функционального ряда
Пусть  сумма ряда (1).
сумма ряда (1).
Определение 2. Функциональный ряд  называется равномерно (правильно) сходящимся в некотором интервале
называется равномерно (правильно) сходящимся в некотором интервале  , если для любого
, если для любого 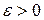 найдется такой номер
найдется такой номер  , что для всех
, что для всех 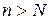 и всех
и всех  выполняется неравенство
выполняется неравенство
 (2)
(2)
Можно сказать, что равномерная сходимость означает, что ряд сходится к своей сумме  одинаково быстро при любом
одинаково быстро при любом  . Особое значение равномерно сходящиеся ряды имеют в связи с тем, что на них переносятся многие свойства конечных сумм. Это следует из теорем:
. Особое значение равномерно сходящиеся ряды имеют в связи с тем, что на них переносятся многие свойства конечных сумм. Это следует из теорем:
Теорема 1. Если члены равномерно сходящегося ряда  являются непрерывными в интервале
являются непрерывными в интервале  функциями переменного
функциями переменного  , то его сумма
, то его сумма  также является непрерывной в этом интервале функцией.
также является непрерывной в этом интервале функцией.
Доказательство. ►Чтобы доказать непрерывность функции  в точке
в точке  , нужно показать, что найдется такая точка
, нужно показать, что найдется такая точка  , что разность
, что разность  будет меньше любого наперед заданного числа
будет меньше любого наперед заданного числа 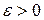 . Исходя из тождества
. Исходя из тождества
 ,
,
где 
 я частичная сумма ряда, составим неравенство
я частичная сумма ряда, составим неравенство
 . (3)
. (3)
Пусть 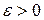 произвольное сколь угодно малое число. Выберем
произвольное сколь угодно малое число. Выберем  настолько близким к
настолько близким к  чтобы одновременно выполнялись неравенства
чтобы одновременно выполнялись неравенства
 ,
,  ,
,  .
.
Справедливость первого и второго неравенств вытекает из равномерной сходимости ряда. Справедливость третьего следует из непрерывности конечных сумм непрерывных функций. Но тогда из (3) немедленно следует
 , (4)
, (4)
что и требовалось доказать. ◄
Теорема 2. Если ряд  сходится к
сходится к  равномерно и его члены интегрируемы в интервале
равномерно и его члены интегрируемы в интервале  то сумма ряда
то сумма ряда  также интегрируема в интервале
также интегрируема в интервале  , причем
, причем
 . (5)
. (5)
Доказательство. ►В силу равномерной сходимости ряда для любого 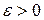 найдется такой номер
найдется такой номер  , что для всех
, что для всех 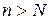 имеет место неравенство (2) при любом
имеет место неравенство (2) при любом  . Но тогда
. Но тогда
 , (6)
, (6)
а это означает, что последовательность частичных сумм  ряда
ряда 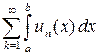 стремится к числу
стремится к числу  , что и требовалось доказать. ◄
, что и требовалось доказать. ◄
Теорема 3. Пусть ряд  сходится к
сходится к  в интервале
в интервале  и его члены непрерывно дифференцируемы в этом интервале. Тогда, если ряд
и его члены непрерывно дифференцируемы в этом интервале. Тогда, если ряд
 , (7)
, (7)
составленный из производных членов исходного ряда, сходится равномерно в интервале  , то сумма ряда
, то сумма ряда  дифференцируема, причем в каждой точке
дифференцируема, причем в каждой точке  справедливо равенство
справедливо равенство
 . (8)
. (8)
Доказательство. ►Обозначим сумму ряда (7)  . В силу предыдущей теоремы имеем равенство
. В силу предыдущей теоремы имеем равенство

или
 .
.
Дифференцирование средней и правой частей этого равенства дает  , ч.т.д. ◄
, ч.т.д. ◄
На практике, для установления равномерной сходимости функционального ряда, удобно применять признак Вейерштрасса:
Теорема 4 (Признак равномерной сходимости Вейерштрасса) Функциональный ряд  сходится равномерно в интервале
сходится равномерно в интервале  , если существует такой сходящийся знакоположительный ряд
, если существует такой сходящийся знакоположительный ряд  , что во всех точках интервала
, что во всех точках интервала  выполняются неравенства
выполняются неравенства  .
.
Доказательство. ►Согласно признаку сравнения ряд  сходится в интервале
сходится в интервале  абсолютно. Пусть
абсолютно. Пусть  его сумма. Тогда для
его сумма. Тогда для  -го остатка ряда можем записать
-го остатка ряда можем записать
 . (9)
. (9)
Так как числовой ряд сходится, то для любого 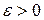 можно найти такой номер
можно найти такой номер  , что
, что  . Но тогда, в силу (9), неравенство
. Но тогда, в силу (9), неравенство  будет иметь место при любом
будет иметь место при любом  из интервала
из интервала  , что и доказывает равномерную сходимость ряда
, что и доказывает равномерную сходимость ряда  . ◄
. ◄
Пример 3. Показать, что ряд  равномерно сходится на всей числовой оси.
равномерно сходится на всей числовой оси.
Решение. Преобразуем общий член ряда воспользовавшись неравенством  , которое выполняется для любых действительных чисел
, которое выполняется для любых действительных чисел  ,
,  :
:
 ,
,
откуда, при  , следует, что
, следует, что
 .
.
Так как неравенство выполняется для всех  , а ряд
, а ряд 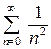 сходится, то исходный ряд равномерно сходится на всей числовой оси.
сходится, то исходный ряд равномерно сходится на всей числовой оси.
Пример 4. Найти сумму ряда  .
.
Указание: Воспользоваться формулой  (см. формулу (32))
(см. формулу (32))
Решение. Пусть  сумма ряда, то есть
сумма ряда, то есть
 .
.
Так как в области сходимости степенной ряд можно почленно дифференцировать, то
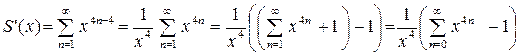
Согласно формуле (32),  , так что:
, так что:
 .
.
Но тогда
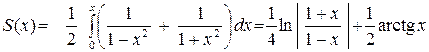 .
.
Лекция 5.
5.1 Степенные ряды
Определение 3. Степенным рядом называется функциональный ряд, вида

 .(10)
.(10)
Числа  называются коэффициентами ряда.
называются коэффициентами ряда.
Вопрос о сходимости степенного ряда решается теоремой Абеля.
Теорема 5. 1). Если степенной ряд (10) сходится при некотором значении 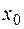 не равном нулю, то он абсолютно сходится при любом значении
не равном нулю, то он абсолютно сходится при любом значении  , таком, что
, таком, что  .
.
2). Если ряд (10) расходится при некотором значении 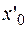 , то он расходится и при всяком
, то он расходится и при всяком  для которого
для которого  .
.
Доказательство. ►1). Так как 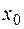 точка сходимости, то числовой ряд
точка сходимости, то числовой ряд
 (11)
(11)
сходится. Следовательно, его общий член  при
при  . Но тогда существует такое положительное число
. Но тогда существует такое положительное число  , что
, что
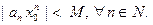 (12)
(12)
Перепишем ряд (11) в виде
 . (13)
. (13)
В силу неравенств (12), члены этого ряда по абсолютной величине меньше членов ряда
 ,
,
представляющего собой геометрическую прогрессию со знаменателем  . Так как прогрессия сходится когда ее знаменатель по модулю меньше единицы, то отсюда следует, что при
. Так как прогрессия сходится когда ее знаменатель по модулю меньше единицы, то отсюда следует, что при  , ряд (13), (а следовательно, и ряд (11)) сходится абсолютно, что и требовалось доказать.
, ряд (13), (а следовательно, и ряд (11)) сходится абсолютно, что и требовалось доказать.
2). Доказательство второй части теоремы очевидно. Если ряд расходится в точке 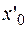 , то он должен расходиться и при любом
, то он должен расходиться и при любом  таком, что
таком, что  , так как в противном случае, в силу первой части теоремы, точка
, так как в противном случае, в силу первой части теоремы, точка 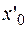 была бы точкой сходимости, что противоречит условию. ◄
была бы точкой сходимости, что противоречит условию. ◄
Следствие. Областью сходимости степенного ряда (11) является интервал 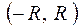 , где
, где  , так называемый, радиус сходимости, с центром в начале координат.
, так называемый, радиус сходимости, с центром в начале координат.
Доказательство. ►Действительно, если 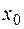 точка сходимости, то все точки интервала
точка сходимости, то все точки интервала  являются точками абсолютной сходимости ряда.. Если
являются точками абсолютной сходимости ряда.. Если 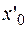 точка расходимости, то все точки интервалов
точка расходимости, то все точки интервалов  ,
,  тоже являются точками расходимости. Но тогда, очевидно, должно существовать такое положительное число
тоже являются точками расходимости. Но тогда, очевидно, должно существовать такое положительное число  , что при
, что при  ряд абсолютно сходится, а при
ряд абсолютно сходится, а при  расходится. ◄
расходится. ◄
Число  , и есть радиус сходимости степенного ряда. Его можно найти, применив к ряду, составленному из абсолютных величин членов ряда (11), например, признак Даламбера. Согласно этому признаку, ряд будет сходиться, если
, и есть радиус сходимости степенного ряда. Его можно найти, применив к ряду, составленному из абсолютных величин членов ряда (11), например, признак Даламбера. Согласно этому признаку, ряд будет сходиться, если
 (14)
(14)
 |
Вычисляя предел, находим
То есть степенной ряд (11) будет сходиться абсолютно при всех  , таких, что
, таких, что  , где
, где  , так что радиус сходимости ряда равен
, так что радиус сходимости ряда равен
 . (15)
. (15)
Вопрос о сходимости ряда на концах интервала сходимости решается индивидуально для каждого из концов. С этой целью следует подставить в ряд значения  и
и  и исследовать сходимость получившихся числовых рядов.
и исследовать сходимость получившихся числовых рядов.
Отметим, что в интервале абсолютной сходимости степенной ряд сходится равномерно. Это следует из теоремы:
Теорема 6. Если степенной ряд
 (*)
(*)
сходится в интервале  и
и  произвольное число такое, что
произвольное число такое, что 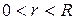 , то в интервале
, то в интервале 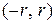 ряд сходится равномерно.
ряд сходится равномерно.
Доказательство. ► Так как степенной ряд сходится абсолютно в любой точке интервала сходимости, то в точке  знакоположительный ряд
знакоположительный ряд
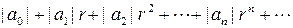 (**)
(**)
сходится. Если  - произвольная точка интервала
- произвольная точка интервала  , то
, то  и ряд (**) является мажорантой для ряда (*) и, следовательно, последний сходится в интервале
и ряд (**) является мажорантой для ряда (*) и, следовательно, последний сходится в интервале  равномерно. ◄
равномерно. ◄
Следствие. В области абсолютной сходимости
а) сумма степенного ряда является непрерывной функцией переменной  ;
;
б) степенной ряд можно почленно дифференцировать;
в) степенной ряд можно почленно интегрировать.
Пример 5. Исследовать сходимость ряда  .
.
Решение. Используя формулу (15), находим радиус сходимости
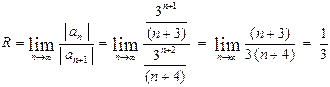 ,
,
то есть ряд абсолютно сходится в интервале  .Исследуем сходимость ряда на концах интервала сходимости: Полагая
.Исследуем сходимость ряда на концах интервала сходимости: Полагая  , получаем расходящийся гармонический ряд
, получаем расходящийся гармонический ряд  .Полагая
.Полагая  , получаем знакочередующийся ряд
, получаем знакочередующийся ряд 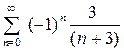 . Этот ряд сходится условно, так как он сходится по признаку Лейбница как знакочередующийся ряд, но ряд составленный из модулей его членов расходится. Итак, рассматриваемый ряд абсолютно сходится в интервале
. Этот ряд сходится условно, так как он сходится по признаку Лейбница как знакочередующийся ряд, но ряд составленный из модулей его членов расходится. Итак, рассматриваемый ряд абсолютно сходится в интервале  и условно сходится в точке
и условно сходится в точке  .
.
5.2 Ряды по степеням разности 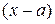
Часто приходится рассматривать степенные ряды по степеням разности 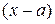 , вида
, вида

 (16)
(16)
Такой ряд заменой переменной 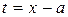 сводится к степенному ряду типа (10). И если область абсолютной сходимости последнего
сводится к степенному ряду типа (10). И если область абсолютной сходимости последнего  , то областью сходимости ряда (16), очевидно, будет интервал
, то областью сходимости ряда (16), очевидно, будет интервал  с центром в точке
с центром в точке  . Сходимость на концах интервала исследуется индивидуально для каждого конца.
. Сходимость на концах интервала исследуется индивидуально для каждого конца.
Пример 6. Исследовать сходимость ряда  .
.
Решение. Применяя признак Даламбера к ряду составленному из модулей членов данного ряда, находим:
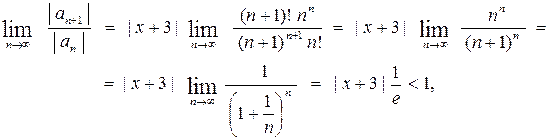
откуда следует, что ряд абсолютно сходится в интервале  . Исследуем сходимость на концах интервала. Пусть
. Исследуем сходимость на концах интервала. Пусть  . Общий член ряда равен
. Общий член ряда равен  . Используя формулу Стирлинга
. Используя формулу Стирлинга 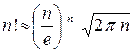 , убеждаемся, что при больших
, убеждаемся, что при больших 
 и не стремится к нулю при
и не стремится к нулю при  , то есть необходимый признак сходимости не выполняется и, следовательно, ряд расходится. Аналогично убеждаемся, что по этой же причине ряд расходится и на втором конце интервала. Таким образом, ряд абсолютно сходится в интервале
, то есть необходимый признак сходимости не выполняется и, следовательно, ряд расходится. Аналогично убеждаемся, что по этой же причине ряд расходится и на втором конце интервала. Таким образом, ряд абсолютно сходится в интервале  и расходится вне него.
и расходится вне него.
Лекция 6.
6.1 Ряды Тейлора и Маклорена
Пусть 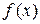 сумма степенного ряда
сумма степенного ряда

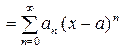 . (17)
. (17)
Выразим его коэффициенты через значения функции 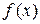 и ее производных в точке
и ее производных в точке  . Последовательно дифференцируя, получаем:
. Последовательно дифференцируя, получаем:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
так, что
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
и ряд (10) принимает вид
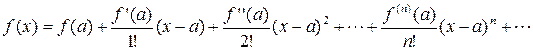 . (18)
. (18)
Пусть теперь 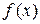 некоторая заданная функция. Если эта функция дифференцируема бесконечное число раз, то для нее могут быть вычислены по приведенным выше формулам коэффициенты
некоторая заданная функция. Если эта функция дифференцируема бесконечное число раз, то для нее могут быть вычислены по приведенным выше формулам коэффициенты  и составлен ряд вида
и составлен ряд вида
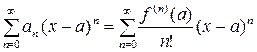 . (19)
. (19)
Этот формально составленный ряд может а) расходиться, б) сходиться, но не к функции  , и, наконец, самый важный для приложений случай, в) сходиться к функции
, и, наконец, самый важный для приложений случай, в) сходиться к функции  . Установить характер сходимости ряда можно с помощью величины
. Установить характер сходимости ряда можно с помощью величины

 (20)
(20)
называемой  м остаточным членом ряда. Доказано, что если для некоторого
м остаточным членом ряда. Доказано, что если для некоторого  выполняется условие
выполняется условие 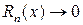 , при
, при  и всех
и всех  таких, что
таких, что 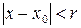 , то ряд (19) сходится к функции
, то ряд (19) сходится к функции  на множестве
на множестве 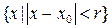 . Для этого случая из (20) получаем
. Для этого случая из (20) получаем
 , (21)
, (21)
при этом остаточный член может быть представлен в виде
 (22)
(22)
где 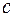 некоторая точка, заключенная между
некоторая точка, заключенная между  и
и  , и называется.
, и называется.  м остаточным членом ряда в форме Лагранжа. Ряд (21) называется рядом Тейлора функции
м остаточным членом ряда в форме Лагранжа. Ряд (21) называется рядом Тейлора функции  . Отметим, что точку
. Отметим, что точку 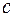 в (22) часто удобнее определять формулой
в (22) часто удобнее определять формулой  , где
, где  - параметр, заключенный в пределах
- параметр, заключенный в пределах  .
.
В частном случае, когда  , ряд (21) принимает вид
, ряд (21) принимает вид
 (23)
(23)
и называется рядом Маклорена. Остаточный член для ряда Маклорена имеет вид:
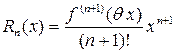 . (24)
. (24)
6.2 Разложение в ряд Маклорена функций 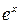 ,
, 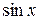 ,
, 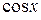 ,
, 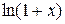
Для дальнейшего будет необходима лемма:
Лемма. При любом конечном 
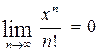 (25)
(25)
Доказательство. ►Пусть, для определенности,  . Рассмотрим ряд с общим членом
. Рассмотрим ряд с общим членом 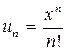 . Этот ряд сходится по признаку Даламбера:
. Этот ряд сходится по признаку Даламбера:

и, следовательно, для него выполняется необходимый признак сходимости, т.е.

что и требовалось доказать. ◄
1). Разложение в ряд Маклорена функции 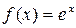 .
.
Значения функции и ее производных в точке 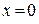 равны:
равны:
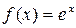 ,
,  ,
,
 ,
, 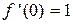 ,
,
 ,
,  ,
,
....................................................................
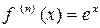 ,
,  ,
,
так что ряд Маклорена принимает вид
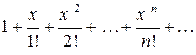 .
.
Радиус сходимости этого ряда
 ,
,
то есть ряд абсолютно сходится на всей числовой оси. Покажем, что остаточный член ряда  стремится к нулю при
стремится к нулю при  . Это будет означать, что ряд имеет суммой
. Это будет означать, что ряд имеет суммой 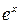 . Действительно,
. Действительно,
 при
при 
в силу леммы. Поэтому
 . (26)
. (26)
2). Разложение в ряд Маклорена функции  .
.
Находим:
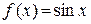 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 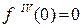
..............................................................................
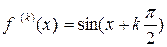 ,
, 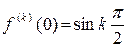
и получаем ряд

в котором члены с четными  отсутствуют. По этой причине удобно положить
отсутствуют. По этой причине удобно положить  ,
,  . Учитывая также, что
. Учитывая также, что
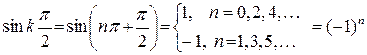
перепишем ряд в виде
 .
.
Покажем, что остаточный член стремится к нулю при  . В самом деле,
. В самом деле,

в силу леммы. Таким образом,
 . (27)
. (27)
Убедитесь, что ряд сходится на всей числовой оси.
3). Разложение в ряд Маклорена функции  .
.
Разложение этой функции в ряд Маклорена проводится аналогично предыдущему и ряд имеет вид
 . (28)
. (28)
4). Разложение в ряд Маклорена функции  .
.
Разложение логарифмической функции в ряд Маклорена проводится по общему правилу, без каких-либо особенностей, и ряд имеет вид
 (29)
(29)
Радиус сходимости этого ряда равен
 .
.
6.3 Разложение в ряд Маклорена функции 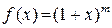 (биномиальный ряд)
(биномиальный ряд)
Вычисляя значения функции и ее производных в точке 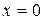 находим:
находим:
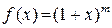 ,
, 
 ,
, 
 ,
, 
 ,
, 
................................................................................................................
 ,
, 
и получаем ряд
 (30)
(30)
где обозначено
 .
.
Если  - целое положительное число, биномиальный ряд вырождается в конечную сумму:
- целое положительное число, биномиальный ряд вырождается в конечную сумму:
 :
:  ,
,
 :
:  ,
,
 :
: 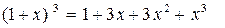 , и т.д.
, и т.д.
Если  не целое положительное число, то число членов в ряде бесконечно. Найдем его интервал сходимости. Воспользовавшись признаком Даламбера, получаем:
не целое положительное число, то число членов в ряде бесконечно. Найдем его интервал сходимости. Воспользовавшись признаком Даламбера, получаем:

откуда и следует, что ряд абсолютно сходится в интервале  . Сходимость на концах интервала сходимости исследуется индивидуально для каждого конца и зависит от значения числа
. Сходимость на концах интервала сходимости исследуется индивидуально для каждого конца и зависит от значения числа  .
.
Приведем важные частные случаи формулы (30).
 (31)
(31)
 . (32)
. (32)
Лекция 7.
7.1 О некоторых приемах разложения функций в степенные ряды
На практике, коэффициенты рядов Тейлора и Маклорена часто находят используя формулы (26) - (32) и применяя различные приемы, такие как: представление заданной функции в виде линейной комбинации основных элементарных функций, замена переменной, почленное дифференцирование и интегрирование рядов, метод неопределенных коэффициентов и др.
Пример 7. Разложить в ряд Маклорена функцию
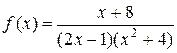 .
.
Решение. Представим функцию  в виде суммы элементарных дробей
в виде суммы элементарных дробей

Сравнивая многочлены в числителях, находим 
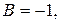
 . Переписывая дробь в виде
. Переписывая дробь в виде

и используя ряды (31) и (32) с соответствующими заменами переменной, получаем:
 .
.
Пример 8. Функцию  разложить в ряд Тейлора в окрестности точки
разложить в ряд Тейлора в окрестности точки  .
.
Решение. Преобразуем функцию:  . Обозначим
. Обозначим  , тогда
, тогда  и
и

Применяя формулу (28), и проводя обратную замену, получаем искомое разложение:

Пример 9. Разложить в ряд Маклорена функцию  .
.
Решение. Воспользуемся интегральным представлением функции и формулой (31)
 .
.
Степенной ряд сходится в интервале  и в этом интервале его можно почленно интегрировать:
и в этом интервале его можно почленно интегрировать:
 ,
,
так, что окончательно:
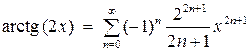 .
.
Область сходимости ряда - интервал  .
.
7.2 Применение рядов для приближенных вычислений
Если некоторая функция  разложена в ряд Тейлора в окрестности точки
разложена в ряд Тейлора в окрестности точки  и
и  — радиус сходимости этого ряда, то для всякого
— радиус сходимости этого ряда, то для всякого 
 имеет место равенство
имеет место равенство
 .
.
Поскольку  при
при  , то при больших
, то при больших  значения многочлена
значения многочлена  отличаются от значений функции
отличаются от значений функции  не более чем на величину
не более чем на величину  которая, в принципе, может быть оценена. На этом факте и основано применение рядов для приближенных вычислений.
которая, в принципе, может быть оценена. На этом факте и основано применение рядов для приближенных вычислений.
7.3 Приближенные вычисления значений функций
Пример 10. Вычислить число  с погрешностью
с погрешностью 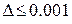 .
.
Решение. Воспользуемся разложением функции 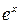 в ряд Маклорена,
в ряд Маклорена,
 ,
,
из которого при  получаем:
получаем:
 .
.
Чтобы определить сколько членов следует взять для достижения требуемой точности, оценим остаточный член  , где
, где  . При
. При  получаем:
получаем:
 ,
,
откуда находим, что уже при  ,
,  . Таким образом,
. Таким образом,
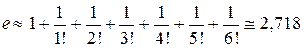 .
.
7.4 Приближенные вычисления интегралов
Пример 11. Вычислить с погрешностью 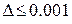 определенный интеграл
определенный интеграл
 .
.
Решение. Используя разложение в ряд Маклорена функции  , получаем ряд:
, получаем ряд:
 .
.
Интегрируя его почленно на отрезке  , находим
, находим




где учтено, что  .
.
Результат представляет собой разность двух сходящихся знакочередующихся рядов. Чтобы обеспечить требуемую точность, каждый из этих рядов должен быть вычислен с погрешностью не более  . Согласно теореме об оценке остатка знакочередующегося ряда, остаток не превышает по величине модуля первого из отбрасываемых членов. Так как
. Согласно теореме об оценке остатка знакочередующегося ряда, остаток не превышает по величине модуля первого из отбрасываемых членов. Так как 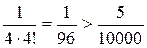 , но
, но 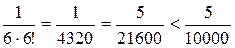 и
и  , а
, а  , то с требуемой точностью, получаем
, то с требуемой точностью, получаем
 .
.
7.5 Решение дифференциальных уравнений
Пусть задано дифференциальное уравнение второго порядка
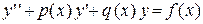 (33)
(33)
и требуется найти его частное решение, удовлетворяющее начальным условиям
 ,
,  . (34)
. (34)
Если функции  представляются степенными рядами вида
представляются степенными рядами вида
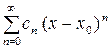 , (35)
, (35)
сходящимися к этим функциям в некоторой окрестности точки  , то существует единственное решение задачи Коши, представимое в виде степенного ряда
, то существует единственное решение задачи Коши, представимое в виде степенного ряда
 , (36)
, (36)
сходящегося в некоторой окрестности точки  .
.
Находя из (36) с помощью дифференцирования степенные ряды для  и
и  , подставляя в уравнение вместо
, подставляя в уравнение вместо  их разложения и производя необходимые арифметические действия над степенными рядами, вместо уравнения (33) получим равенство двух степенных рядов. Из этого равенства можно последовательно найти коэффициенты ряда (36) и, тем самым получить решение задачи Коши.
их разложения и производя необходимые арифметические действия над степенными рядами, вместо уравнения (33) получим равенство двух степенных рядов. Из этого равенства можно последовательно найти коэффициенты ряда (36) и, тем самым получить решение задачи Коши.
Пример 12. Решить задачу Коши для дифференциального уравнения
 , если
, если 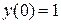 ,
,  .
.
Решение. Ищем решение уравнение в виде ряда
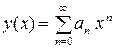 . (37)
. (37)
Тогда
 , (38)
, (38)
 ,
,
и уравнение принимает вид
 . (39)
. (39)
Сравнивая коэффициенты при одинаковых степенях  , находим
, находим
 ,
,  .
.
Так как  , то из рекуррентной формулы следует
, то из рекуррентной формулы следует  ,
,  и вообще,
и вообще,
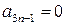 . (40)
. (40)
Из этой же формулы получаем
 ,
, 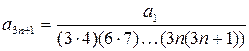 . (41)
. (41)
Из начальных условий, следует  ,
, 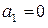 и с помощью формул (40), (41) находим частное решение
и с помощью формул (40), (41) находим частное решение
 , (42)
, (42)
удовлетворяющее заданным начальным условиям. Можно показать, что ряд сходится при любых  .
.
Лекция 8.
Ряды Фурье.
8.1 Тригонометрический ряд. Ряд Фурье
Определение 1. Функциональный ряд вида
 (1)
(1)
называется тригонометрическим рядом.
Если ряд сходится, то его сумма - периодическая функция с периодом  (в силу периодичности функций
(в силу периодичности функций  и
и  ).
).
Пусть  - сумма тригонометрического ряда то есть
- сумма тригонометрического ряда то есть
 2017-11-01
2017-11-01 313
313