Профессионального образования

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего

профессионального образования

“ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ”

______________________________________________________________

 

Черкасов М.Р.

 

 

ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ,

РЯДЫ ФУРЬЕ,

ИНТЕГРАЛ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ

 

Курс лекций

 

 

Томск 2008

Оглавление

Лекция 1. Числовые ряды

1.1Понятие числового ряда. Сходимость и сумма ряда

1.2 Геометрическая прогрессия

1.3 Свойства числовых рядов

1.4 Необходимый признак сходимости ряда

Лекция 2.

2.1 Достаточные признаки сходимости знакоположительных рядов

2.2 Признаки сравнения

2.3 Признак Даламбера

2.4 Радикальный признак Коши

2.5 Интегральный признак Коши

Лекция 3.

3.1 Знакопеременные ряды

3.2 Знакочередующиеся ряды

3.3 Произвольные знакопеременные ряды. Абсолютная и условная сходимость

3.4 Остаток ряда и его оценка

Лекция 4. Функциональные ряды

4.1Понятие функционального ряда. Область сходимости

4.2 Равномерная (правильная) сходимость функционального ряда

Лекция 5.

5.1 Степенные ряды

5.2 Ряды по степеням разности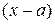

Лекция 6.

6.1 Ряды Тейлора и Маклорена

6.2 Разложение в ряд Маклорена функций , , ,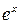

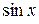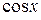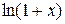
6.3 Разложение в ряд Маклорена функции 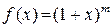(биномиальный ряд)

Лекция 7.

7.1 О некоторых приемах разложения функций в степенные ряды

7.2 Применение рядов для приближенных вычислений

7.3 Приближенные вычисления значений функций

7.4 Приближенные вычисления интегралов

7.5 Решение дифференциальных уравнений

Лекция 8. Ряды Фурье

8.1 Тригонометрический ряд. Ряд Фурье

8.2 Условия разложимости функции в ряд Фурье

Лекция 9.

9.1 Ряды Фурье для четных и нечетных функций

9.2 Разложение в ряды Фурье функций с периодом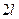

9.3 Разложение в ряды Фурье непериодических функций

9.4 Некоторые приложения рядов Фурье

Лекция 10. Интеграл и преобразование Фурье

10.1 Интеграл Фурье

10.2 Преобразование Фурье

Литература

Лекция 1.

Числовые ряды

1.1 Понятие числового ряда. Сходимость и сумма ряда

Пусть числа

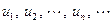, (1)

образуют последовательность.

Определение. Числовым рядом называется сумма членов числовой последовательности, т. е.:

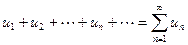, (2)

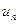- общий член ряда.

Подчеркнем, что как следует из определения, ряд представляет собой сумму бесконечного числа слагаемых. Как будет видно из дальнейшего, следствием именно этого факта являются некоторые особенности, принципиально отличающие ряды от конечных сумм. Ряд считается заданным, если общий член известен как функция его номера. Приведем примеры числовых рядов:

1). ,

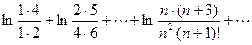2). ,

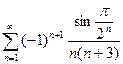3). .

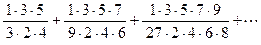В первых двух примерах общий член ряда известен. Именно, в первом примере

,

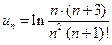а во втором

.

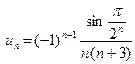В третьем же примере общая закономерность, которой подчиняются члены ряда устанавливается тремя первыми членами и чтобы ряд можно было считать заданным, следует проанализировать их и установить функциональную зависимость общего члена ряда от его номера . Замечаем, что в числителях стоят произведения нечетных чисел от единицы до 5 в первом члене, до 7 во втором и до 9 в третьем. Все эти числа могут быть воспроизведены выражением 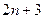при, соответственно, 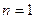, 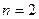и 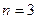. То есть, числитель в общем члене может быть представлен выражением 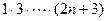. В знаменателе, как нетрудно заметить, первый сомножитель отличается от остальных, представляющих собой последовательную запись четных чисел. Установление закономерности, связывающей числа в знаменателе с номером члена, несложно и находим, что знаменатель может быть описан выражением 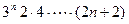, так что общий член этого ряда принимает вид

.

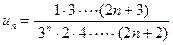Запись этой формулы можно сделать более компактной, если воспользоваться двойным факториалом. Именно, согласно определению двойного факториала 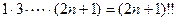и 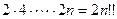, так что

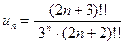
и ряд может быть записан в виде

.

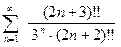Определение. Сумма первых членов ряда называется -ой частичной суммой ряда, т.е.:

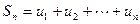(3)

Выпишем частичные суммы ряда (1):

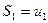
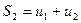
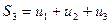
(4)

.

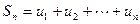
Частичные суммы образуют последовательность, при этом, очевидно, чем больше , тем ближе -ая частичная сумма ряда 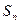к сумме ряда 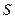. Поэтому естественно следующее определение суммы ряда:

Определение. Суммой числового ряда называется предел последовательности его частичных сумм, т. е.

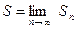(5)

Если указанный предел существует и конечен, то говорят, что ряд сходится и имеет сумму .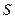

Если предел бесконечен или не существует, то говорят, что ряд расходится.