Интеграл и преобразование Фурье

 

10.1 Интеграл Фурье

Пусть функция определена в бесконечном интервале и абсолютно интегрируема на нем, т.е. существует и конечен интеграл

. (50)

Пусть также на любом конечном интервале функция удовлетворяет условиям теоремы Дирихле и, следовательно, разложима на нем в ряд Фурье, т.е., при любом конечном справедливы формулы (39) – (42). Подставляя в ряд (39) вместо коэффициентов правые части формул (40) – (42), получим:

(51)

Перепишем эту формулу в следующем виде

(52)

Воспользовавшись, далее, формулой

, (53)

получим:

(54)

Прежде чем переходить к пределу 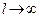, введем обозначения

, (55)

и перепишем формулу (54) в виде

(56)

 

При первое слагаемое в (56) стремится к нулю. Действительно,

Второе слагаемое представляет собой интегральную сумму для функции

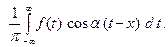
Поэтому, переходя к пределу , вместо ряда получим интеграл

, (57)

называемый интегралом Фурье. Отметим, что равенство (57) имеет место во всех точках непрерывности функции .В точках разрыва интеграл Фурье равен полусумме предельных значений функции слева и справа, то есть

. (58)

 

Преобразуем интеграл в (57), вновь воспользовавшись формулой (53):

(59)

Вводя обозначения

,

(60)

вместо (59) получим

. (61)

Совершенно очевидна аналогия с тригонометрическим рядом – параметр , пробегавший значения чисел натурального ряда, заменен на непрерывно меняющийся параметр , а бесконечный ряд заменен интегралом. Коэффициенты и по своей структуре также напоминают коэффициенты Фурье. Определяющие их интегралы существуют, так как из абсолютной интегрируемости функции

на всей числовой оси следует и абсолютная интегрируемость функций и .

Рассмотрим частные случаи формулы (59).

1). Пусть - четная функция. Тогда - четная, а - нечетная функции, следовательно

, (62)

. (63)

Интеграл Фурье для четной функции, таким образом, принимает вид

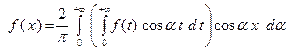. (64)

2). Если функция нечетная, то четная, а нечетная функции и в этом случае

, (65)

(66)

и интеграл Фурье имеет вид

. (67)

Итак, четные функции разлагаются в ряд Фурье по косинусам, а нечетные по синусам.

 

10.2 Преобразование Фурье

Формулы (64) и (67) могут быть представлены в симметричной форме. Именно, вместо формулы (64) можно записать

, 68)

. (69)

Эти формулы называются, соответственно, прямым и обратнымкосинус - преобразованием Фурье. Заметим, что каждую из этих формул можно рассматривать как интегральное уравнение относительно функции, стоящей под знаком интеграла. При этом вторая формула дает решение этого уравнения.

Аналогично, формула (67) эквивалентна двум формулам

, (70)

, (71)

которые называются, соответственно, прямым и обратнымсинус - преобразованием Фурье.

Отметим, что синус и косинус преобразования могут применяться лишь к функциям, заданным на положительной полуоси, абсолютно интегрируемым на ней и удовлетворяющим на любом ее конечном интервале условиям Дирихле.

Пример. Для функции найти косинус и синус преобразования Фурье.

Решение. Задача решается непосредственно по формулам (68) и (70). При этом предполагается, что в область отрицательных значений аргумента функция продолжается в первом случае четным а во втором нечетным образом. Согласно формуле (68):

Вычислим интеграл, применяя метод интегрирования по частям:

 

 

Итак, мы получили: , отсюда следует , так что окончательно

.

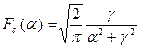Синус преобразование находится аналогично и имеет вид:

.▲

 

Л И Т Е Р А Т У Р А

1. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. — М: «Интеграл-Пресс», 1998.

2. Никольский С.М. Курс математического анализа. Т.2.. — М: «Наука», 1983.

3. Кудрявцев Л. Д. Курс математического анализа. Т.2.. — М: «высшая школа», 1981.

4. Ильин В. А., Позняк Э.Г. Основы математического анализа. Т.2.. — М: «Наука», 1980.

5. Зорич В. А. Математический анализ. Т.2. — М: «Наука», 1984

6. Демидович Б. П. Сборник задач и упражнений по математическому анализу.. — М: «Наука», 1977.

7. Берман Г. Н. Сборник задач по курсу математического анализа.. — М: «Наука», 1985.

8. Задачи и упражнения по математическому анализу для втузов /Под ред. Демидовича Б.П.. — М: «Наука», 1972.

9. Сборник задач по математике для втузов. Специальные разделы математического анализа. /Под ред. Ефимова А.В. и Демидовича Б.П... — М: «Наука», 1986.

10. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин В.И. Сборник задач по математическому анализу. Интегралы. Ряды.. — М: «Наука», 1986.

11. Данко П. Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.2.. — М: «Высшая школа», 1996.

 

 

[1] Каждый его член, начиная со второго, является средним гармоническим двух соседних членов. Число называется средним гармоническим чисел и, если, например,