Геометрическая прогрессия

1 2 3 4 5 6

, (21)

которая сходится при , и расходится при ,

и обобщенный гармонический ряд ( ряд Дирихле)

, (22)

который, как будет показано ниже, сходится при показателе , и расходится при .

При этот ряд принимает вид

(23)

и называется гармоническим рядом. [1]

Пример 4. Исследовать сходимость ряда .

Решение. Поскольку и ряд с общим членом расходится, то, по признаку сравнения, расходится и рассматриваемый ряд

Пример 5. Исследовать сходимость ряда .

Решение. Воспользуемся тождеством: (для доказательства которого достаточно прологарифмировать его обе части) и тем фактом, что возрастающая функция и при достаточно больших 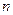справедливо неравенство , тогда

и так как обобщенный гармонический ряд с показателем сходится, то по признаку сравнения сходится и данный ряд.

Пример 6. Исследовать сходимость ряда .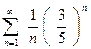

Решение. Поскольку , и представляет собой общий член сходящейся геометрической прогрессии (со знаменателем ), то рассматриваемый ряд также сходится.

2). Предельный признак сравнения

Теорема. Если при предел отношения общих членов рядов

(24)

(25)

существует и конечен т.е.

и , (26)

то оба ряда (u) и (v) сходятся или расходятся одновременно.

Доказательство. ► Пусть предел (26) существует и конечен, т. е. . Тогда для любого положительного числа при достаточно больших 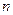будет выполняться неравенство

или

(27)

Пусть ряд (v) сходится. Тогда из неравенства 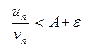следует и так как по теореме 1 ряд с общим членом тоже сходится, то по признаку сравнения сходится и ряд . Пусть теперь ряд расходится. Тогда из неравенства 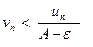и признака сравнения следует, что будет расходиться и ряд с общим членом , а значит, в соответствии с теоремой 1, и ряд .Теорема доказана. ◄

Согласно необходимому признаку сходимости ряда, если ряд сходится, то его общий член стремится к нулю при , то есть является бесконечно малой величиной при . Поэтому для сходящихся рядов предел (26) эквивалентен утверждению, общие члены рядов и при 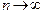являются бесконечно малыми одного порядка. Поскольку, как мы знаем, обобщенный гармонический ряд с общим членом сходится при , то отсюда вытекает следствие:

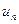Следствие. Если при общий член ряда

является бесконечно малой величиной более высокого порядка чем , то есть если существует такое положительное число , что имеет место

, (28)

то данный ряд сходится.

Пример 7. Исследовать сходимость ряда .

Решение. Составляя предел (28), находим:

и, например, при получаем

то есть общий член ряда при является бесконечно малой более высокого порядка чем 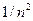и, в соответствии со следствием к предельному признаку сравнения, этот ряд сходится.

Замечание. В качестве контрпримера приведем ряд . С одной стороны

а, с другой

при любом . То есть с одной стороны, при величина стремится к нулю быстрее чем , но с другой стороны она не является бесконечно малой более высокого порядка чем . Это объясняется тем, что при функция стремится к бесконечности, но медленнее чем любая положительная степень .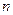

2.3 Признак Даламбера

Теорема. Если при предел отношения -го члена ряда

к 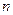-му существует, конечен и равен ,то есть

, (29)

то при ряд сходится, при расходится, а при вопрос о сходимости ряда остается открытым и нужно применить другой признак.

. Доказательство. ► Пусть предел (29) существует, конечен и . Покажем, что ряд сходится. Из определения предела следует, что для любого положительного числа найдется такой номер 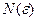, что для всех 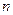больших будет выполняться неравенство

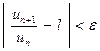
или

Выберем настолько малым, чтобы было

Тогда для всех

или:

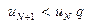
Рассмотрим теперь два ряда:

Второй из них представляет собой геометрическую прогрессию со знаменателем и, следовательно, сходится. Но тогда, поскольку члены первого ряда меньше соответствующих членов второго ряда, по признаку сравнения он тоже сходится. Так как этот ряд получен из исходного ряда путем отбрасывания его первых членов, что не влияет на сходимость ряда, то исходный ряд тоже сходится.

Пусть теперь то есть . Но тогда, для достаточно больших 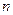, , а это означает, что общий член ряда не стремится к нулю при , то есть для этого ряда не выполняется необходимый признак сходимости и такой ряд, следовательно, не может быть сходящимся. Теорема доказана. ◄

Пример 8. Исследовать сходимость ряда .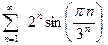

Решение. Воспользуемся признаком Даламбера. Имеем:

Вычисляя предел (29), находим:

при этом была использована эквивалентность бесконечно малых величин: . Так как предел меньше единицы, то рассматриваемый ряд сходится.

Пример 9. Исследовать сходимость ряда .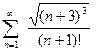

Решение. Применим признак Даламбера. Имеем:

и предел (29) равен

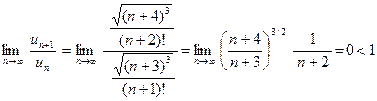(было использовано свойство факториала ). Так как предел меньше единицы, то данный ряд сходится.

2.4 Радикальный п ризнак Коши

Теорема. Если для знакоположительного ряда

существует и конечен предел

, (30)

Д оказательство. ► Пусть предел (30) существует, конечен и . Покажем, что ряд сходится. Из определения предела следует, что для любого положительного числа найдется такой номер 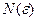, что для всех 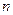больших будет выполняться неравенство

или

Выберем настолько малым, чтобы было . Тогда для всех будет справедливо неравенство , или Рассмотрим два ряда

Второй из них представляет собой геометрическую прогрессию со знаменателем и, следовательно, сходится. Но тогда, поскольку члены первого ряда меньше соответствующих членов второго ряда, то, по признаку сравнения, он тоже сходится. Так как этот ряд получен из исходного ряда путем отбрасывания его первых членов, что не влияет на сходимость ряда, то исходный ряд тоже сходится.

Пусть теперь , то есть . Но тогда, начиная с некоторого номера , будет иметь место неравенство , или . Последнее означает, что общий член ряда не стремится к нулю при , то есть для этого ряда не выполняется необходимый признак сходимости и такой ряд, следовательно, не может быть сходящимся. Теорема доказана. ◄

Пример 10. Исследовать сходимость ряда .

Решение. Воспользуемся радикальным признаком Коши:

Так как предел меньше единицы, то ряд сходится. При решении примера был использован второй замечательный предел 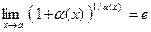, где 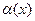бесконечно малая при .

2.5 Интегральный п ризнак Коши

Теорема. Пусть члены знакоположительного ряда

(31)

являются значениями непрерывной неотрицательной и монотонно убывающей на полуинтервале функции при целочисленных значениях ее аргумента, т. е.

тогда: если сходится несобственный интеграл 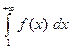, то сходится и ряд, если несобственный интеграл 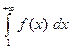расходится, то расходится и ряд.

. Доказательство. ► В соответствии с условием теоремы рассматриваемый ряд может быть представлен в виде

Пусть какая-либо первообразная функции , и так как , то возрастает с ростом и при имеет предел, конечный или бесконечный. Введем в рассмотрение числовую последовательность . Тогда, в первом случае последовательность сходится, т. е.: , где 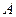- конечно, а значит, сходится и ряд

= , (32)

поскольку его сходимость эквивалентна существованию предела варианты . Во втором случае последовательность расходится и расходится ряд (32). С этим рядом и сравним рассматриваемый ряд.

По формуле конечных приращений Лагранжа, общий член ряда (32) может быть представлен в виде

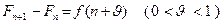, (33)

так что вследствие монотонности функции имеем:

и тогда, в случае сходимости интеграла сходится ряд (32), а значит, по признаку сравнения, сходится и ряд (31), так как его общий член меньше общего члена сходящегося ряда (32). Если же интеграл расходится, то расходится ряд (32), а значит и ряд (31) так как его общий член больше общего члена расходящегося ряда (32). Теорема доказана. ◄

Пример 11. Исследовать сходимость обобщенного гармонического ряда .

Решение. Воспользуемся интегральным признаком Коши. Введем функцию и рассмотрим несобственный интеграл при . Имеем:

то есть при интеграл расходится, а при сходится. Если , то

то есть интеграл тоже расходится. Таким образом, в соответствии с интегральным признаком Коши, обобщенный гармонический ряд сходится при и расходится при .

Пример 12. Исследовать сходимость ряда .

Решение. Воспользуемся вновь интегральным признаком Коши. Полагая , находим:

и так как интеграл расходится, то расходится и ряд.

Лекция 3.

3.1 Знакопеременные ряды

Определение. Числовой ряд, среди членов которого имеются как положительные, так и отрицательные числа, называется знакопеременным рядом

Пример:

3.2 Знакочередующиеся ряды

Среди знакопеременных рядов особое значение имеют знакочередующиеся ряды

Определение. Числовой ряд, в котором за каждым положительным членом следует отрицательный, а за каждым отрицательным - положительный, называется знакочередующимся рядом.

Пример:

В дальнейшем условимся записывать знакочередующийся ряд в виде

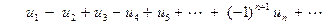, (34)

считая числа положительными, но подчеркнем, что там, где стоит знак минус, членами ряда являются именно отрицательные числа .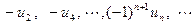

Для знакочередующихся рядов существует следующий достаточный признак сходимости.

Признак Лейбница

Теорема. Если члены знакочередующегося ряда

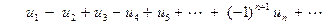
по абсолютной величине убывают т. е.

, (35)

и его общий член стремится к нулю при , т. е.

, (36)

то этот ряд сходится, его сумма положительна и не превышает по величине первого члена ряда.

Доказательство. Рассмотрим частичную сумму четного числа членов ряда

Сгруппируем ее члены попарно следующим образом

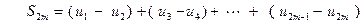В силу неравенств (35), все слагаемые в скобках положительны, так что и возрастает с ростом . Сгруппируем теперь члены в по-другому:

Сумма в квадратных скобках, очевидно, положительна, и поэтому .

Итак, мы показали, что последовательность четных сумм возрастает с ростом , оставаясь ограниченной. Следовательно, она имеет предел

и так как ,

Рассмотрим частичную сумму нечетного числа членов ряда, и так как

находим:

так как по условию (а значит и ). Поскольку, последовательности четных и нечетных частичных сумм имеют один и тот же предел 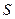, то и , причем, . Теорема доказана. ◄

Замечание. Так как добавление или отбрасывание конечного числа первых членов не изменяет сходимости ряда, то для сходимости знакочередующегося ряда достаточно чтобы неравенства (35) имели место начиная с некоторого . Убывание членов ряда по абсолютной величине начиная с первого члена ряда необходимо для того чтобы можно было сделать заключение о том, что сумма ряда положительна и не превышает по величине первого члена ряда.

Пример 13. Доказать сходимость ряда .

Решение. Действительно, члены данного ряда по абсолютной величине убывают

и его общий член стремится к нулю при ,

то есть ряд удовлетворяет признаку Лейбница и, следовательно, сходится.

Перейдем к рассмотрению произвольных знакопеременных рядов. Будем записывать такой ряд в виде

где числа могут быть как положительными, так и отрицательными.

3.3 Произвольные знакопеременные ряды. Абсолютная и условная сходимость

Для произвольных знакопеременных рядов существует следующий достаточный признак сходимости.

Теорема. Если для знакопеременного ряда

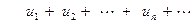(37)

сходится ряд

, (38)

составленный из абсолютных величин его членов, то данный знакопеременный ряд тоже сходится.

Доказательство. Пусть

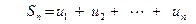
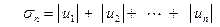
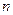-е частичные суммы рядов (37) и (38). Обозначим через сумму всех положительных, а через - всех отрицательных слагаемых среди первых членов в ряде(37). Тогда, очевидно:

Так как по условию теоремы ряд (38) сходится, то есть существует и конечен предел

и имеют конечные пределы последовательности частичных сумм и т. е.

, .

и при этом

Но тогда имеет конечный предел и :

откуда и следует сходимость ряда (37). Теорема доказана. ◄

Рассмотренный признак сходимости является достаточным, но не необходимым. То есть существуют сходящиеся знакопеременные ряды, для которых этот признак не выполняется. В качестве примера приведем ряд

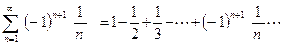который сходится по признаку Лейбница, поскольку

и ,

но ряд, составленный из модулей его членов, является расходящимся гармоническим рядом.

Определение Знакопеременный ряд

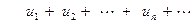
называется абсолютно сходящимся рядом, если сходится ряд, составленный из модулей его членов, и называется условно сходящимся, если он сходится как знакопеременный ряд, но ряд составленный из модулей его членов расходится.

Среди знакопеременных рядов абсолютно сходящиеся ряды выделяются тем, что на них переносятся все свойства конечных сумм. В частности имеет место переместительное свойство:

сумма абсолютно сходящегося ряда не меняется при любой перестановке его членов.

В случае условно сходящихся рядов переставлять члены нельзя (речь идет о перестановке бесконечного числа членов) – это может не только изменить сумму ряда но и сделать ряд расходящимся.

Пример. Обратимся вновь к ряду 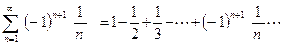, сходящемуся, как было показано выше, условно. Пусть 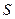- его сумма. Перегруппируем члены ряда следующим образом:

и выпишем частичные суммы исходного и этого ряда:

и вообще, можно показать, что , и так как , и, поскольку , то предел последовательности частичных сумм существует и . Таким образом, проведенная перегруппировка членов условно сходящегося ряда привела к изменению его суммы.