Побудова кумулятативної кривої. Знаходження числових характеристик вибірки

Мета: навчитися знаходити статистичні (емпіричні) функції розподілу частот для дискретних і неперервних ознак, будувати кумулятативні криві; обчислювати числові характеристики дискретної ознаки.

 

Статистична функція розподілу частот. Кумулятативна крива.

Статистичною(емпіричною) функцією розподілу називається функція , яка для кожного значення 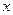визначає відносну частоту появи події (ознаки) , тобто , де 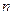– обсяг у вибірки, а – накопичені частоти варіант, які менші заданої варіанти .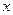

а) Нехай для дискретної кількісної ознаки задана частотна таблиця:

				...
				...

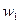
(1)

 

 

Згідно з означенням функції для дискретної ознаки маємо .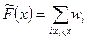

Отже, функцію можна записати так:

Графік цієї функції має вигляд:

1

 

 

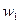
0 х₁ х₂ х₃ х_к-1 х_к х_і

 

Тут точки розриву графіка функції – варіанти ознаки, а величини стрибків в кожній точці розриву – це відносні частоти варіант.

б) Нехай для неперервної кількісної ознаки задається інтервальна частотна таблиця:

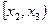
В цьому випадку значення функції обчислюється в кінцях часткових інтервалів таким чином:

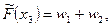
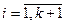
Побудувавши на площині точки (), і сполучивши їх ламаною лінією, дістанемо графік функції який називається кумулятативною кривою:

1

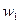
0 х₁ х₂ х₃ х_к х_к+1 х_і