Б) Інтервальне оцінювання параметрів розподілу

Оцінка називається інтервальною, якщо вона визначається двома числами – кінцями інтервалу.

Такою оцінкою слід користуватися при великому обсязі вибірки.

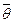Точкові оцінки, розглянуті вище, не завжди співпадають з істинними значеннями невідомих параметрів розподілу. Отже, є деяка похибка при заміні невідомого параметра його оцінкою , тобто .

Величина похибки, при цьому, невідома, хоча хотілось би знати, до яких помилок може привести заміна параметра його точковою оцінкою.

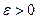Точністю оцінки називається число , для якого .

Зрозуміло, чим менше , тим точнішою буде оцінка. Проте, статистичні методи не дозволяють категорично стверджувати, що оцінка задовольняє нерівність; можна лише говорити про ймовірність, з якою ця нерівність здійснюється.

Надійністю (надійним рівнем) оцінки параметра називається ймовірність , з якою здійснюється нерівність , тобто

ще називають довірча ймовірність.

Як правило, число задається наперед і береться рівним 0,95; 0,99; 0,999, тобто числом, близьким до 1.

Надійним (довірчим) інтервалом називається інтервал , який з ймовірністю ”Накриває” (містить в собі) невідомий параметр .

Числа та 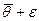називається надійними (довірчими) межами для параметра .

Розглянемо на прикладі зміст, який має задана надійність ρ. Так надійність 0,95 означає, що якщо проведена достатньо велика кількість вибірок, то 95% з них визначають такі надійні інтервали, які покривають оцінюваний параметр θ і лише в 5% випадків він може вийти за межі довірчого інтервалу. Тому, якщо ρ вибирається близьким до 1, то можна бути практично впевненим, що в одиничній серії випробувань надійний інтервал “накриє” параметр θ.

Метод визначення надійних інтервалів був розроблений американським статистиком Ю.Непманом, виходячи з ідеї англійського статистика Р.Фішера.