Розглядаємо першу задачу теорії кореляції. Нехай ознаки  і
і  зв’язані лінійною кореляційною залежністю. Вважатимемо, що різні значення
зв’язані лінійною кореляційною залежністю. Вважатимемо, що різні значення  ознаки
ознаки  і відповідні їм значення
і відповідні їм значення  ознаки
ознаки  спостерігаються по одному разу. За результатами випадкової вибірки
спостерігаються по одному разу. За результатами випадкової вибірки  ,
,  з генеральної сукупності шукається вибіркове рівняння прямої лінії регресії у вигляді
з генеральної сукупності шукається вибіркове рівняння прямої лінії регресії у вигляді 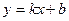 , де
, де  і
і 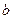 - невідомі параметри,
- невідомі параметри, 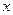 - кутовий коефіцієнт, що називається вибірковим коефіцієнтом регресії
- кутовий коефіцієнт, що називається вибірковим коефіцієнтом регресії  на
на  .
.
Для обчислення значень параметрів вибраного рівняння регресії найчастіше користуються методом найменших квадратів. Сутність цього методу полягає в тому, що сума квадратів відстаней експериментальних точок від найбільш ймовірної кривої є найменшою (звідси і назва методу).
Для розв’язання цієї задачі потрібно визначити точку мінімуму функції
 .
.
Знайшовши похідні функції 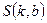 і прирівнявши їх до нуля, після відповідних перетворень одержується система рівнянь:
і прирівнявши їх до нуля, після відповідних перетворень одержується система рівнянь:
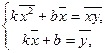 де
де
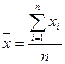 ,
,  ,
,  ,
,  .
.
Параметр  можна знайти, наприклад, за формулою Крамера
можна знайти, наприклад, за формулою Крамера
 , де
, де 
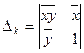 .
.
Тоді  .
.
 2017-10-25
2017-10-25 1249
1249








