Решение инженерных задач с использованием условий равновесия жидкости и твёрдого тела в жидкости

Задача 3.1.

Рис.3.1.

Определить диаметр поплавка, имеющего вес , который при слое воды обеспечивал бы автоматическое открытие клапана диаметром . Длина тяги , вес клапана и тяги составляет . Плотность воды и ускорение свободного падения принять равными .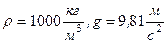

 

Решение.

Составляем условие равновесия поплавка

.

Диаметр поплавка

,

Ответ: .

Задача 3.2.

Рис.3.2.

Грунтовые воды, формирующие систему с нефтяным пластом, выходят на поверхность (рис.). Определить плотность глинистого, раствора, применяемого для бурения , чтобы предотвратить фонтанирование нефти при вскрытии пласта. Глубина скважины ; расстояния ; плотность подземных вод 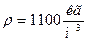; плотность нефти .

 

 

Решение.

Составим уравнение равновесия системы «грунтовые воды нефть»:

, следовательно .

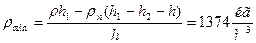Ответ: .

Задача 3.3.

Рис.3.3.

Цистерна, из цилиндрической части, длиной , и двумя полусферами, радиуса , заполнена нефтепродуктом плотностью . Толщина стенок цистерны , а плотность материала . Какова должна быть максимальная масса нефтепродукта в цистерне, что бы она не затонула в воде?

 

Решение.

На плавающую цистерну действуют 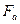- сила Архимеда, - вес цистерны, - вес нефтепродукта, уравнение равновесия имеет вид:

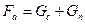
или

,

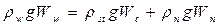здесь 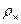-плотность воды, - объемы вытесненной воды, стенок цистерны, нефтепродукта, соответственно.

Найдем объемы цистерны (вытесненной воды), внутренний объем цистерны и ее стенок:

,

,

.

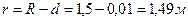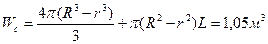Вычислим силу Архимеда, вес цистерны, вес нефтепродукта и его объем:

,

,

.

Теперь можно определить максимальную массу и объем нефтепродукта, позволяющего цистерне остаться на плаву:

.

Ответ: .

Задача 3.4.

Рис.3.4.

Цилиндрическая цистерна диаметром 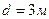, заполнена «под крышку», высотой 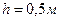, нефтепродуктом с плотностью . Определить величину силы действующей на торцевые стенки цистерны и точку ее приложения .

 

Решение.

Задача сводится к определению гидростатической силы, действующей на плоскую круглую поверхность, расположенную вертикально. Модуль гидростатической силы , а сама она направлена горизонтально. Глубина центра масс , площадь стенки , тогда . Глубина центра давления , момент инерции , Окончательно: .

 

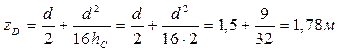Ответ: , .

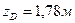Задача 3.5.

Рис.3.5

Прямоугольное отверстие в плоской стенке резервуара , закрыто плоской крышкой на шарнире . Определить силу давления воды на крышку , вертикальную координату центра давления , силу 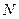, удерживающую крышку на расстоянии 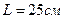от шарнира. Если расстояние от кромки отверстия до поверхности воды 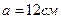, ширина крышки , а давление на манометре . Атмосферное давление и ускорение свободного падения принять равными .

 

Решение. На крышку действует сила абсолютного давления жидкости, причем в ее создании участвует только поверхность отверстия, контактирующая с водой в баке. Ее можно определить по формуле:

,

где: 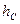- глубина центра масс отверстия, - площадь отверстия. Вычислим силу:

, ,

.

Данная сила приложена в точке - центре давления отверстия. Найдем глубину центра давления:

,

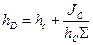где - момент инерции относительно оси проходящей через центр масс отверстия, который равен , тогда:

.

Крышка удерживается силой внешнего давления и силой 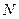, - атмосферное давление, - площадь крышки.

, .

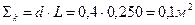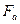Вычисли моменты сил и относительно оси .

,

.

Внешнее давление не обеспечивает закрытие крышки. Определим величину дополнительной силы 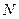. Сумма моментов всех сил, действующих на крышку равна нулю:

Ответ: .

Задача 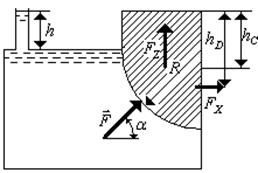3.6.

Рис.3.6.

Определить силу давления на цилиндрическую стенку водяного резервуара, а также угол ее наклона , если ее радиус и ширина 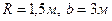, высота уровня воды в пьезометре .

Решение. Разложим силу на проекции . Первую силу можно определить, как силу действующую на проекцию стенки на вертикальную плоскость, перпендикулярную плоскости рисунка. Она представляет собой прямоугольник . Тогда:

.

.

Силу 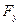можно вычислить через объем тела давления, которое показано на рисунке как заштрихованная область.

Ответ: .

Задача 3.7.

Рис.3.7.

Два плунжера, находящиеся в горизонтальной плоскости, уравновешены. Определить показания манометра и силу , если сила . Пощади сечения плунжеров , .

Решение. Согласно закону Паскаля давление в горизонтальной плоскости одинаковое и равно манометрическому.

Сила уравновешивающая второй плунжер

Ответ: , .

Задача 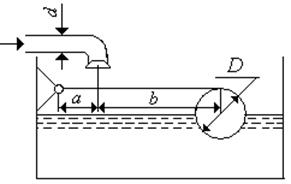3.8.

Рис.3.8.

Определить минимально необходимый диаметр шарового поплавка , обеспечивающего автоматическое закрытие клапана при на­полнении резервуара, если вода под давлением 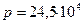Па заполняет резервуар через трубу диаметром d = 15 мм, при а = 15 мм и b = 500 мм. Собственной массой рычага, клапана и поплавка пренебречь

Ответ: .