91-100. Исследовать методами дифференциального исчисления функцию  и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
91.  . 96.
. 96.  .
.
92. 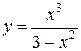 . 97.
. 97.  .
.
93. 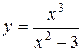 . 98.
. 98. 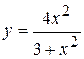 .
.
94.  . 99.
. 99.  .
.
95.  . 100.
. 100. 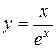 .
.
Пример.  .
.
1. Область определения:  .
.
2. 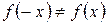 ,
,  , -следовательно, функция не является четной, нечетной, периодической.
, -следовательно, функция не является четной, нечетной, периодической.
3. Исследуем характер точки разрыва  и поведение функции вблизи этой точки:
и поведение функции вблизи этой точки:
 ,
,
 .
.
Таким образом, в точке  функция терпит разрыв второго рода, а прямая
функция терпит разрыв второго рода, а прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
4. Определим уравнение наклонной асимптоты:
 , где
, где
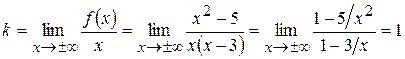 ,
,
 .
.
Итак,
 -наклонная асимптота.
-наклонная асимптота.
5. Определим критические точки.
 ,
,
 при
при  или
или  , то есть при
, то есть при  или
или  , - других критических точек в области определения функции нет. Значения функции в критических точках:
, - других критических точек в области определения функции нет. Значения функции в критических точках:
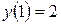 ,
,  .
.
6. Найдем вторую производную:
 .
.
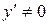 , следовательно, точек перегиба нет.
, следовательно, точек перегиба нет.
7. Внесем все полученные данные в таблицу, определим поведение функции на различных участках и построим график.
| x | 
| 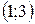
| 
| 
| |||

| + | - | - | + | |||

| - | - | - | + | + | + | |
    y y
| max | min |
Положительные значения первой производной соответствуют промежуткам возрастания, отрицательные – промежуткам убывания. Положительные значения второй производной соответствуют промежуткам вогнутости функции, отрицательные – промежуткам выпуклости. Точка, в которой возрастание функции сменяется убыванием, является точкой максимума, а точка, в которой убывание функции сменяется возрастанием – точкой минимума.

 2017-10-25
2017-10-25 632
632








